24.1.2垂直于弦的直径(第2课时)

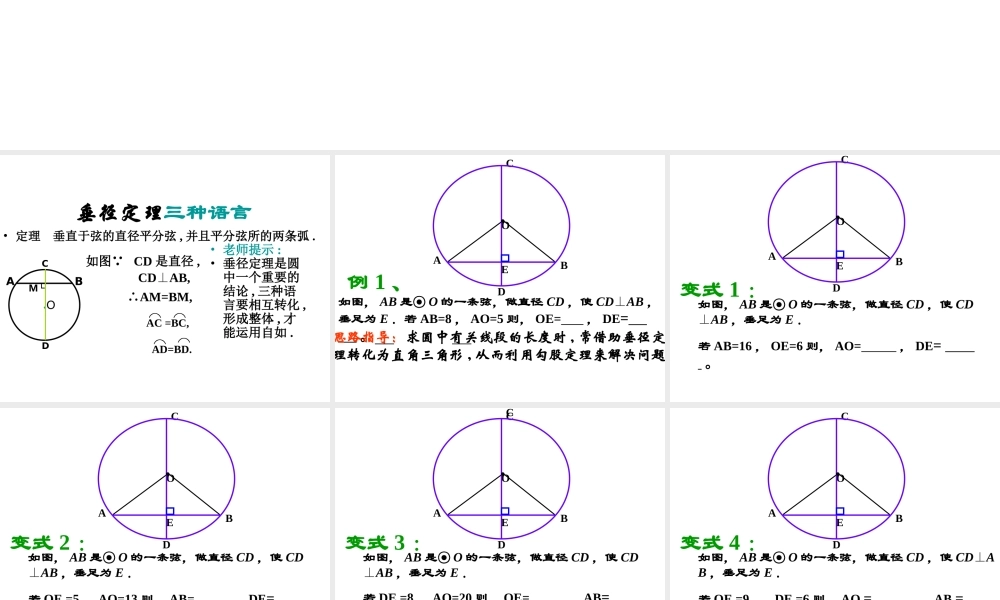
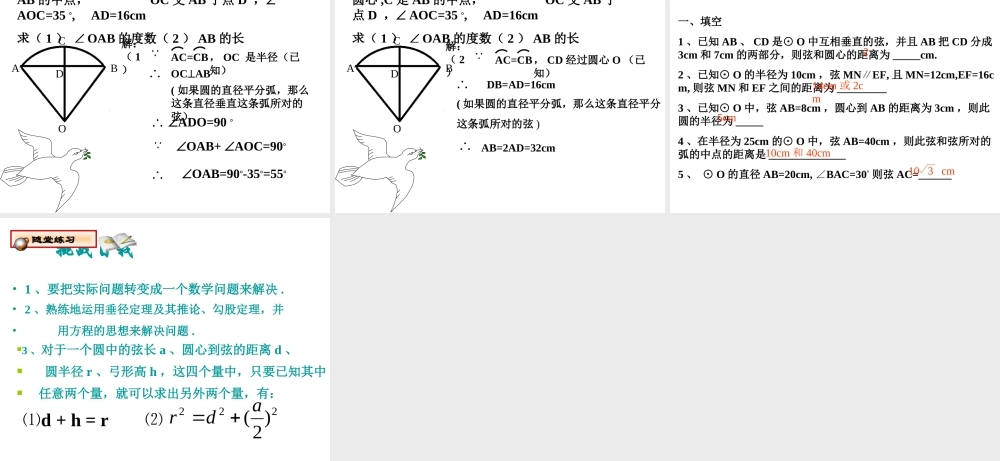
§ 24.1.2 垂直于弦的直径（ 第 2 课时） 重点、难点：垂径定理及其推论的应用垂径定理三种语言• 定理 垂直于弦的直径平分弦 , 并且平分弦所的两条弧 .• 老师提示 :• 垂径定理是圆中一个重要的结论 , 三种语言要相互转化 ,形成整体 , 才能运用自如 .●OABCDM└CDAB,⊥如图 CD 是直径 ,∴AM=BM,⌒ ⌒ AC =BC,⌒ ⌒ AD=BD.如图， AB 是⊙ O 的一条弦，做直径 CD ，使 CD⊥AB ，垂足为 E ．若 AB=8 ， AO=5 则， OE= ， DE= 。 思路指导：求圆中有关线段的长度时 , 常借助垂径定理转化为直角三角形 , 从而利用勾股定理来解决问题 . BCOAED.例 1 、BCOAED.如图， AB 是⊙ O 的一条弦，做直径 CD ，使 CD⊥AB ，垂足为 E ．若 AB=16 ， OE=6 则， AO= ， DE= 。 变式 1 ：如图， AB 是⊙ O 的一条弦，做直径 CD ，使 CD⊥AB ，垂足为 E ．若 OE =5 ， AO=13 则， AB= ， DE= 。BCOAED.变式 2 ：C如图， AB 是⊙ O 的一条弦，做直径 CD ，使 CD⊥AB ，垂足为 E ．若 DE =8 ， AO=20 则， OE= ， AB= 。 BCOAED.变式 3 ：如图， AB 是⊙ O 的一条弦，做直径 CD ，使 CD⊥AB ，垂足为 E ．若 OE =9 ， DE =6 则， AO = ， AB = 。BCOAED.变式 4 ：如图， AB 是⊙ O 的一条弦，做直径 CD ，使 CD⊥AB ，垂足为 E ．若 AB=40 ， DE=10 ，则 OE= ， AO= 。 BCOAED.变式 5 ：小结：在圆的半径，弦长，弦心距及拱高四个量中，只要已知两个量，我们就可以借助勾股定理求出另外的两个量。E例 2 已知：如图１，在以 O为圆心的两个同心圆中，大圆的弦 AB 交小圆于 C ， D 两点。求证： AC ＝ BD 。.ACDBO垂径定理的应用讲解图１解决有关弦的问题时，经常连结半径；过圆心作一条与弦垂直的线段等辅助线，为应用垂径定理创造条件。方法归纳：变式 1 ：如图： OA=OB ，AC=BD 吗？为什么？.ACDBO图２变式变式 22 ：：如图： OA=OB ，AC=BD 吗？为什么？ACDBO图３已知⊙ O 的半径为 10 ，弦 AB∥CD ， AB=12 ， CD=16 ，则 AB 和 CD 的距离为 ． 2 或 14提高练习 :.O.OADCBABCD解：（ 1）AC=CB， OC 是半径（已知）OCAB( 如果圆的直径平分弧，那么这条直径垂直这条弧所对的弦） ADO=90 OAB+ AOC=90OAB=90-35...