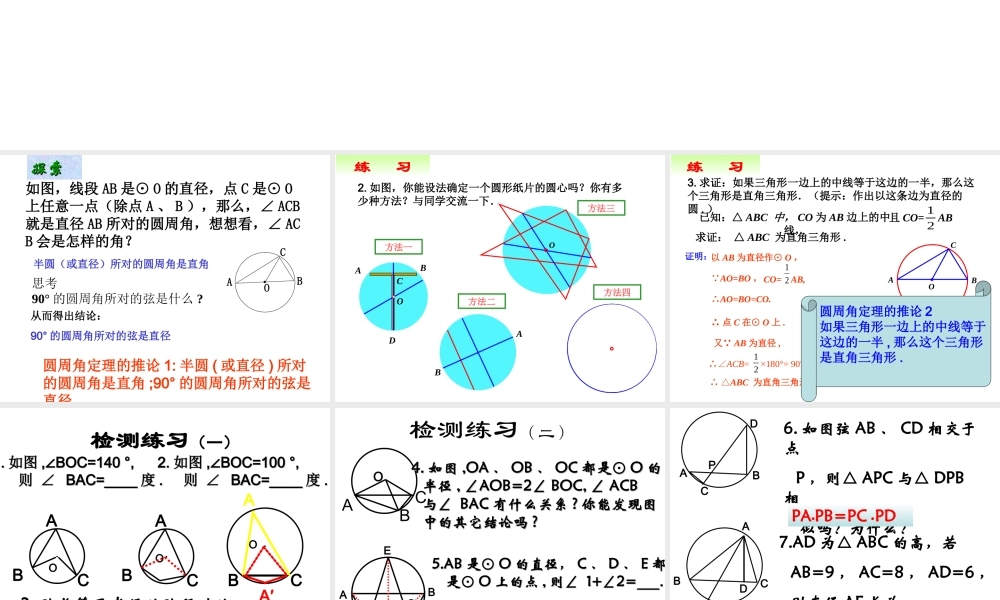
§ 24.1.4 圆周角(第 2 课时)重点:圆周角定理推论难点:圆周角定理及其推论的应用知识点 : 圆周角定理的两个推论探索探索如图,线段 AB 是⊙ O 的直径,点 C 是⊙ O上任意一点(除点 A 、 B ),那么,∠ ACB就是直径 AB 所对的圆周角,想想看,∠ ACB 会是怎样的角?OCBA思考90° 的圆周角所对的弦是什么 ? 从而得出结论:90° 的圆周角所对的弦是直径半圆(或直径)所对的圆周角是直角圆周角定理的推论 1: 半圆 ( 或直径 ) 所对的圆周角是直角 ;90° 的圆周角所对的弦是直径 .2. 如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DABCOOO·方法一方法二方法三方法四AB练 习3. 求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆 . )·ABCO求证: △ ABC 为直角三角形 .证明:CO= AB,12以 AB 为直径作⊙ O , AO=BO ,∴AO=BO=CO.∴ 点 C 在⊙ O 上 .又 AB 为直径 ,∴∠ACB= ×180°= 90°.12已知:△ ABC 中, CO 为 AB 边上的中线,12且 CO= AB ∴ △ABC 为直角三角形 .练 习圆周角定理的推论 2如果三角形一边上的中线等于这边的一半 , 那么这个三角形是直角三角形 .检测练习(一)●OCBA1.1. 如图如图 , BOC=140 °,∠, BOC=140 °,∠ 则 ∠则 ∠ BAC=____BAC=____ 度度 ..●OCBA2.2. 如图如图 , BOC=100 °,∠, BOC=100 °,∠ 则 ∠则 ∠ BAC=____BAC=____ 度度 ..3. 弦长等于半径的弦所对的 圆周角为 _____ 度 .●OCBAA′ 检测练习 ( 二 )OCAB4.4. 如图如图 ,OA,OA 、、 OBOB 、、 OCOC 都是⊙都是⊙ OO 的的 半径半径 , ∠AOB=2∠, ∠AOB=2∠ BOC, ∠BOC, ∠ ACB ACB 与∠与∠ BACBAC 有什么关系有什么关系 ?? 你能发现图你能发现图 中的其它结论吗中的其它结论吗 ??12DCBAE5.AB5.AB 是⊙是⊙ OO 的直径,的直径, CC 、、 DD 、、 EE 都都 是⊙是⊙ OO 上的点上的点 ,, 则∠ 则∠ 1+∠2=___.1+∠2=___.FDCBAP6. 如图弦 AB 、 CD 相交于点 P ,则△ APC 与△ DPB相 似吗?为什么?DCBAE7.AD 为△ ABC 的高,若 AB=9 , AC=8 , AD=6 , 则直径 AE 长为 _______.PA●PB=PC ● PDAB● AC=h ● 2r如图 , ⊙O 的直径 AB 为 10 cm ,弦 AC 为6 cm...