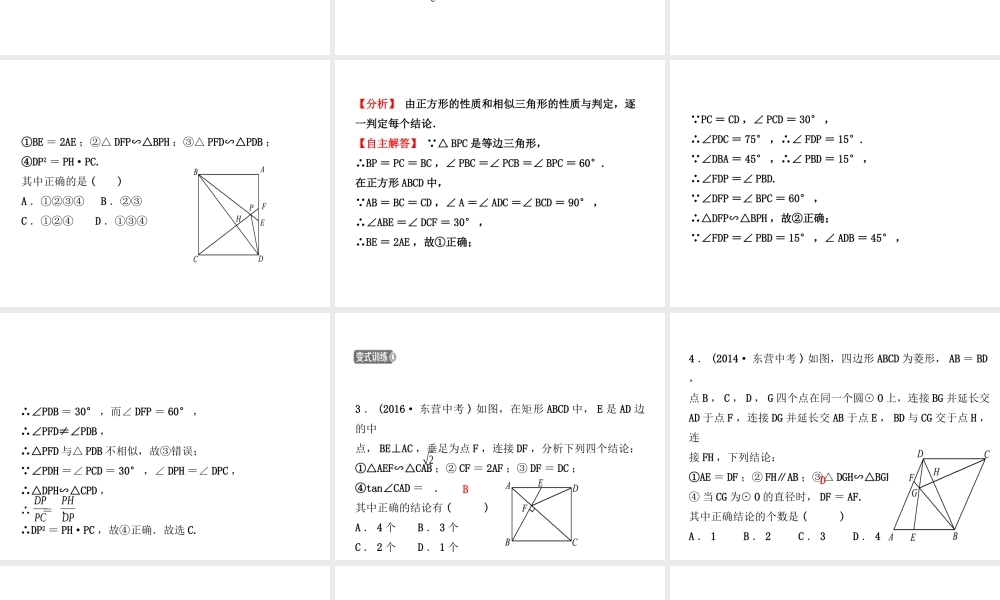
第七节 相似三角形考点一 比例的有关概念与性质 (5 年 1 考 )例 1(2018· 嘉兴中考 ) 如图,直线 l1∥l2∥l3 ,直线 AC 交 l1,l2 , l3 于点 A , B , C ;直线 DF 交 l1 , l2 , l3 于点 D , E, F ,已 知= ,则 = .ABAC13EFDE【分析】 根据题意求出 ,根据平行线分线段成比例定理解答.【自主解答】 = ,∴ = 2. l1∥l2∥l3 , ∴ = = 2.故答案为 2. BCABABAC13BCABEFDEBCAB利用平行线分线段成比例解题的易错点利用平行线分线段成比例解题时,关键是准确找出图形中的对应线段,正确列出比例式求解、计算.容易触雷的地方有: (1) 比例的对应线段找不准; (2) 比例的性质掌握不牢,无法进行转化.1 . (2015· 东营中考 ) 若 = ,则 的值为( )yx34xyxD2 . (2017· 临沂中考 ) 如图,已知 AB∥CD , AD 与 BC 相交于点 O. 若 = , AD = 10 ,则 AO = .BOOC234 考点二 相似三角形的性质与判定 (5 年 5 考 )命题角度 与四边形有关的综合性选择题❶例 2 (2017· 东营中考 ) 如图,在正方形 ABCD 中,△ BPC 是等边三角形, BP , CP 的延长线分别交 AD 于点 E , F ,连接 BD,DP , BD 与 CF 相交于点 H. 给出下列结论:①BE = 2AE ;②△ DFP∽△BPH ;③△ PFD∽△PDB ;④DP2 = PH·PC.其中正确的是 ( )A .①②③④B .②③C .①②④D .①③④【分析】 由正方形的性质和相似三角形的性质与判定,逐一判定每个结论.【自主解答】 △ BPC 是等边三角形,∴BP = PC = BC ,∠ PBC =∠ PCB =∠ BPC = 60°.在正方形 ABCD 中, AB = BC = CD ,∠ A =∠ ADC =∠ BCD = 90° ,∴∠ABE =∠ DCF = 30° ,∴BE = 2AE ,故①正确; PC = CD ,∠ PCD = 30° ,∴∠PDC = 75° ,∴∠ FDP = 15°. ∠DBA = 45° ,∴∠ PBD = 15° ,∴∠FDP =∠ PBD. ∠DFP =∠ BPC = 60° ,∴△DFP∽△BPH ,故②正确; ∠FDP =∠ PBD = 15° ,∠ ADB = 45° ,∴∠PDB = 30° ,而∠ DFP = 60° ,∴∠PFD≠∠PDB ,∴△PFD 与△ PDB 不相似,故③错误; ∠PDH =∠ PCD = 30° ,∠ DPH =∠ DPC ,∴△DPH∽△CPD , ∴ = ,∴DP2 = ...