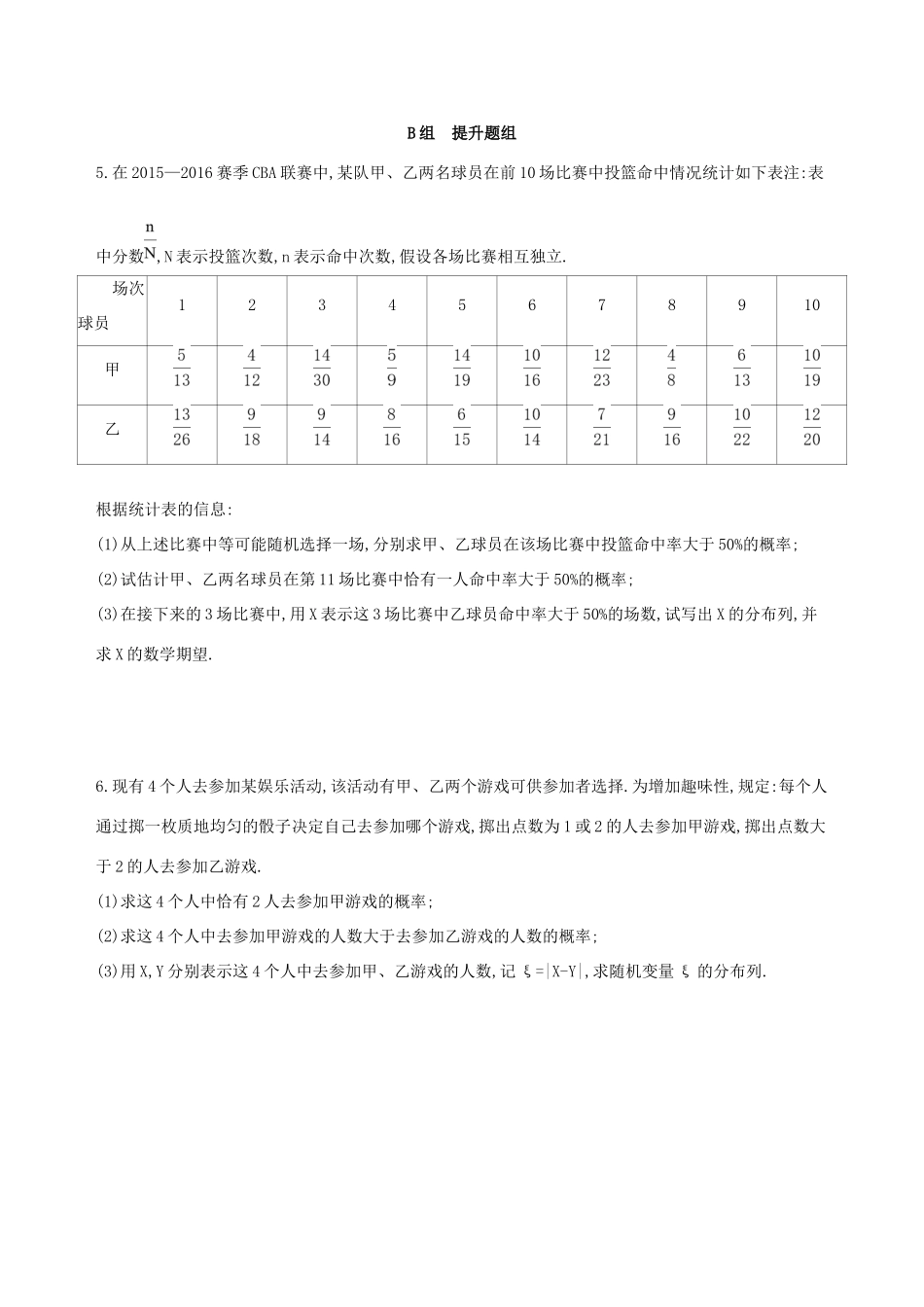
第七节n次独立重复试验与二项分布A组基础题组1.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.3122.把一枚硬币连续抛两次,记“第一次出现正面”为事件A,“第二次出现正面”为事件B,则P(B|A)等于()A.B.C.D.3.我校要用三辆校车从本校区把教师接到东校区,已知从本校区到东校区有两条公路,校车走公路①堵车的概率为,不堵车的概率为;校车走公路②堵车的概率为p,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.(1)若三辆校车中恰有一辆校车被堵的概率为,求走公路②堵车的概率;(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列.4.已知某种动物服用某种药物一次后当天出现A症状的概率为.某小组为了研究连续服用该药物后出现A症状的情况,进行了药物试验.试验设计为每天用药一次,连续用药四天为一个用药周期.假设每次用药后当天是否出现A症状与上次用药无关.(1)如果出现A症状即停止试验,求试验至多持续一个用药周期的概率;(2)如果在一个用药周期内出现3次或4次A症状,则在这个用药周期结束后终止试验,试验至多持续两个周期.设药物试验持续的用药周期为η,求η的期望.B组提升题组5.在2015—2016赛季CBA联赛中,某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表注:表中分数,N表示投篮次数,n表示命中次数,假设各场比赛相互独立.场次球员12345678910甲乙根据统计表的信息:(1)从上述比赛中等可能随机选择一场,分别求甲、乙球员在该场比赛中投篮命中率大于50%的概率;(2)试估计甲、乙两名球员在第11场比赛中恰有一人命中率大于50%的概率;(3)在接下来的3场比赛中,用X表示这3场比赛中乙球员命中率大于50%的场数,试写出X的分布列,并求X的数学期望.6.现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,规定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.(1)求这4个人中恰有2人去参加甲游戏的概率;(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X-Y|,求随机变量ξ的分布列.答案精解精析A组基础题组1.A该同学通过测试的概率P=×0.62×0.4+0.63=0.432+0.216=0.648,故选A.2.AP(B|A)===.3.解析(1)由题意得××·(1-p)+·p=,即3p=1,则p=.(2)ξ可能的取值为0,1,2,3.P(ξ=0)=××=;P(ξ=1)=;P(ξ=2)=××+·××=;P(ξ=3)=××=.所以ξ的分布列为Ξ0123P4.解析(1)解法一:记用药持续i天为事件Ai,i=1,2,3,4,用药至多持续一个周期为事件B,所以P(A1)=,P(A2)=×,P(A3)=×,P(A4)=×,则P(B)=P(A1)+P(A2)+P(A3)+P(A4)=.解法二:记用药至多持续一个周期为事件B,则为用药持续超过一个周期,所以P()==,所以P(B)=1-=.(2)随机变量η的所有可能取值为1,2,所以P(η=1)=·+=,P(η=2)=1-=,所以Eη=1×+2×=.B组提升题组5.解析(1)根据投篮统计数据知,在10场比赛中,甲球员投篮命中率大于50%的场次有5场,所以在随机选择的一场比赛中,甲球员的投篮命中率大于50%的概率是.在10场比赛中,乙球员投篮命中率大于50%的场次有4场,所以在随机选择的一场比赛中,乙球员的投篮命中率大于50%的概率是.(2)设在一场比赛中,甲、乙两名球员恰有一人命中率大于50%为事件A,甲球员命中率大于50%且乙球员命中率不大于50%为事件B1,乙球员命中率大于50%且甲球员命中率不大于50%为事件B2,则P(A)=P(B1)+P(B2)=×+×=.(3)X的可能取值为0,1,2,3.P(X=0)==;P(X=1)==;P(X=2)==;P(X=3)==.X的分布列如下表:X0123PEX=3×=.6.解析依题意,这4个人中,每个人去参加甲游戏的概率都为,去参加乙游戏的概率都为.设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),则P(Ai)=·.(1)这4个人中恰有2人去参加甲游戏的概率P(A2)=×=.(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则B=A3∪A4.由于A3与A4互斥,故P(B)=P(A3)+P(A4)=×+=.所以这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为.(3)ξ的所有可能取值为0,2,4.由于A1与A3互斥,A0与A4互斥,故P(ξ=0)=P(A2)=,P(ξ=2)=P(A1)+P(A3)=,P(ξ=4)=P(A0)+P(A4)=.所以ξ的分布列是ξ024P