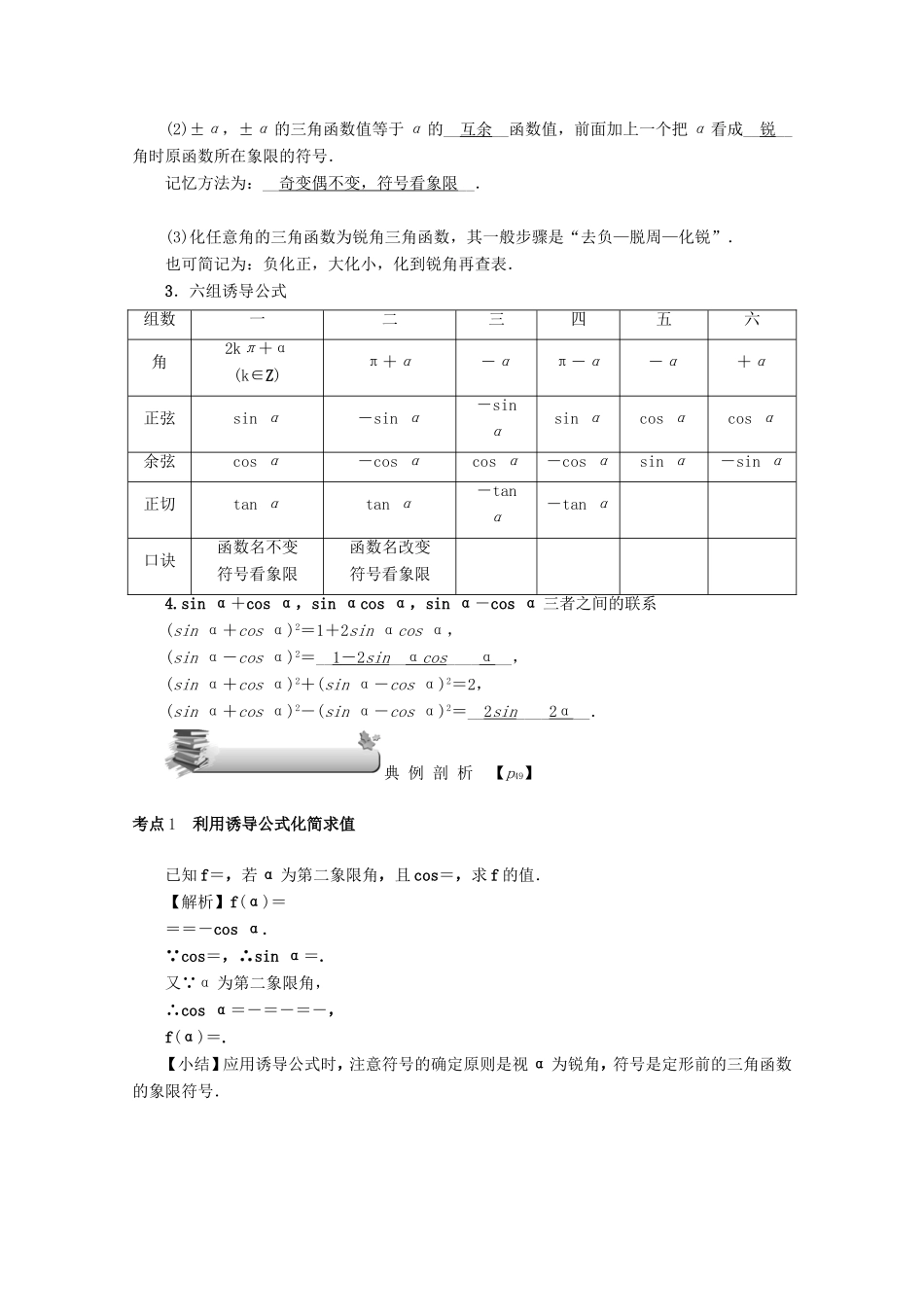
第20讲同角三角函数的基本关系与诱导公式夯实基础【p49】【学习目标】1.掌握同角三角函数的基本公式.2.掌握正弦、余弦的诱导公式.【基础检测】1.已知α是第二象限角,sinα=,则cosα等于()A.-B.-C.D.【解析】 sinα=,α是第二象限角,∴cosα=-=-.【答案】B2.已知cos(π+α)=-,且α为第四象限角,则sin(2π-α)=()A.-B.C.D.-【解析】由题cos(π+α)=-,且α为第四象限角,则cos(π+α)=-cosα=-,∴cosα=,sinα=-,sin(2π-α)=-sinα=.选B.【答案】B3.若tanθ=2,则sin2θ+sinθcosθ-2cos2θ=()A.B.C.D.【解析】原式====,故选B.【答案】B4.已知sinx+cosx=,且00,cosx<0,∴cosx-sinx<0,cosx-sinx=-=-=-.【答案】B【知识要点】1.同角三角函数的基本关系(1)平方关系:__sin2α+cos2α=1__.(2)商数关系:__tan__α=__.2.诱导公式(1)2kπ+α(k∈Z),-α,π±α,2π-α的三角函数值等于α的__同名__函数值,前面加上一个把α看成__锐__角时原函数所在象限的符号.(2)±α,±α的三角函数值等于α的__互余__函数值,前面加上一个把α看成__锐__角时原函数所在象限的符号.记忆方法为:__奇变偶不变,符号看象限__.(3)化任意角的三角函数为锐角三角函数,其一般步骤是“去负—脱周—化锐”.也可简记为:负化正,大化小,化到锐角再查表.3.六组诱导公式组数一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sinα-sinα-sinαsinαcosαcosα余弦cosα-cosαcosα-cosαsinα-sinα正切tanαtanα-tanα-tanα口诀函数名不变符号看象限函数名改变符号看象限4.sinα+cosα,sinαcosα,sinα-cosα三者之间的联系(sinα+cosα)2=1+2sinαcosα,(sinα-cosα)2=__1-2sin__αcos____α__,(sinα+cosα)2+(sinα-cosα)2=2,(sinα+cosα)2-(sinα-cosα)2=__2sin____2α__.典例剖析【p49】考点1利用诱导公式化简求值已知f=,若α为第二象限角,且cos=,求f的值.【解析】f(α)===-cosα. cos=,∴sinα=.又 α为第二象限角,∴cosα=-=-=-,f(α)=.【小结】应用诱导公式时,注意符号的确定原则是视α为锐角,符号是定形前的三角函数的象限符号.考点2利用同角三角函数公式化简、求值(1)已知sin+2cos=0,则=()A.3B.-3C.D.-【解析】因为sin+2cos=0,所以-sinθ-2cosθ=0,可得tanθ=-2,===,故选C.【答案】C(2)若α是第二象限角,则tanα化简的结果是()A.-1B.1C.-tan2αD.tan2α【解析】因为α是第二象限角,所以tanα=tanα=tanα=tanα×=-1.【答案】A【小结】(1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tanα可以实现角α的弦切互化.(2)应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.考点3运用“sinα±cosα”与“sinαcosα”的关系求值已知关于x的方程2x2-(+1)x+m=0的两根为sinα与cosα,α∈,求α及m.【解析】由根与系数的关系可得将①式两边同时平方,得1+2sinαcosα=,sinαcosα=.由②得=,m=,方程可化为2x2-(+1)x+=0,x=或x=. α∈,∴sinα=,cosα=.故α=.【小结】本题充分利用根与系数关系及三角函数基本关系式.【能力提升】(1)在△ABC中,sin=3sin(π-A),且cosA=-cos(π-B),则C等于________.【解析】 sin=3sin(π-A),∴cosA=3sinA,即tanA=.又 A∈(0,π),∴A=.由cosA=-cos(π-B),得cosA=cosB.∴cosB=,又B∈(0,π),∴B=.故C=π--=.【答案】(2)已知定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[-3,-2]上是减函数,若α,β是锐角三角形的两个内角,则()A.f>fB.ffD.f