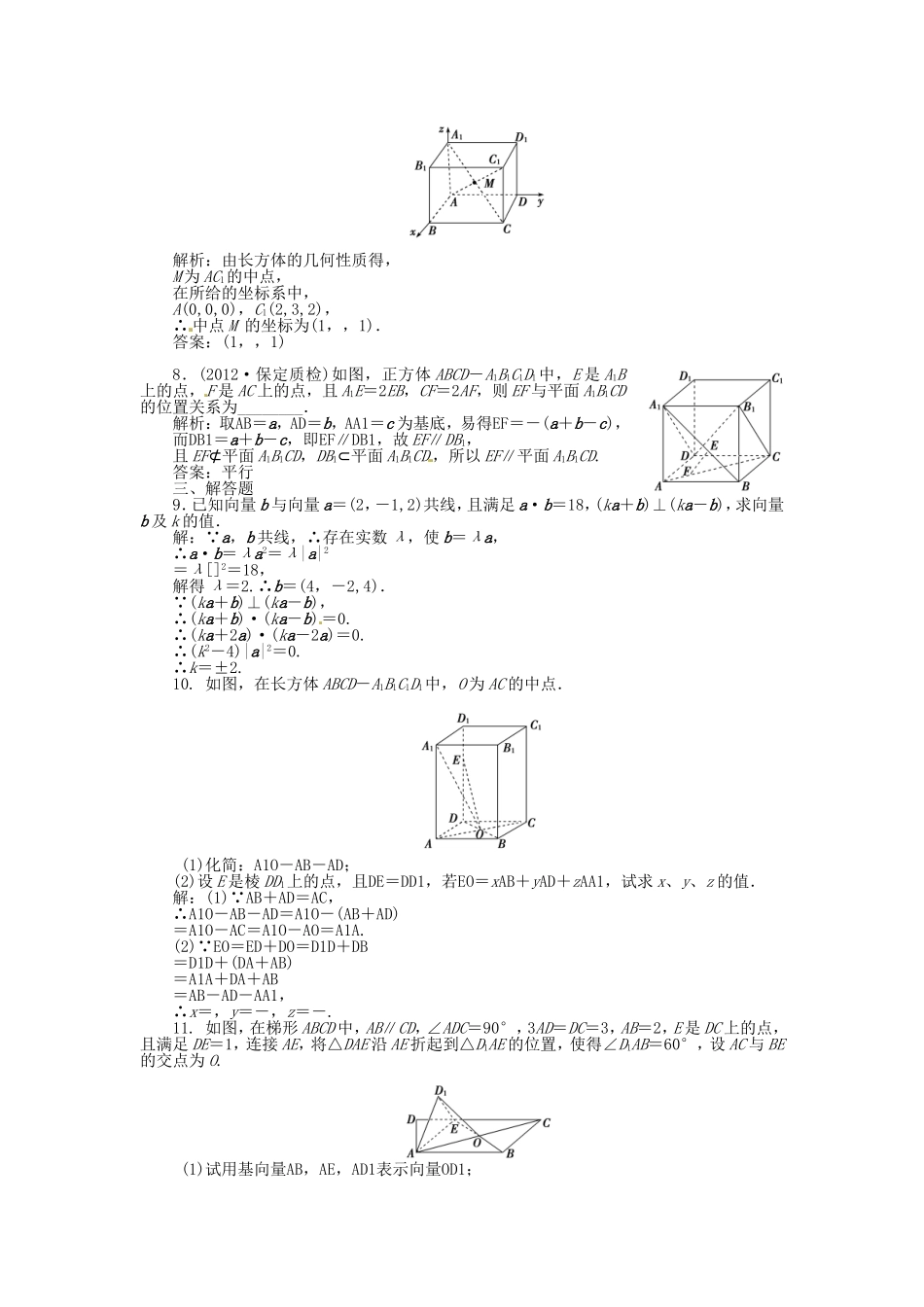
一、选择题1.空间直角坐标系中,A(1,2,3),B(-2,-1,6),C(3,2,1),D(4,3,0),则直线AB与CD的位置关系是()A.垂直B.平行C.异面D.相交但不垂直解析:选B.由题意得AB=(-3,-3,3),CD=(1,1,-1),∴AB=-3CD,∴AB与CD共线,又AB与CD没有公共点.∴AB∥CD.2.已知O,A,B,C为空间四个点,又OA,OB,OC为空间的一个基底,则()A.O,A,B,C四点不共线B.O,A,B,C四点共面,但不共线C.O,A,B,C四点中任意三点不共线D.O,A,B,C四点不共面解析:选D.OA,OB,OC为空间的一个基底,所以OA,OB,OC不共面,但A,B,C三种情况都有可能使OA,OB,OC共面.3.已知两空间向量m=(cosθ,1,sinθ),n=(sinθ,1,cosθ),则m+n与m-n的夹角是()A.B.-C.D.解析:选A.由题意得(m+n)·(m-n)=m2-n2=cos2θ+1+sin2θ-(sin2θ+1+cos2θ)=0,∴(m+n)⊥(m-n),∴〈m+n,m-n〉=.4.空间四点A(2,3,6)、B(4,3,2)、C(0,0,1)、D(2,0,2)的位置关系为()A.共线B.共面C.不共面D.无法确定解析:选C.∵AB=(2,0,-4),AC=(-2,-3,-5),AD=(0,-3,-4).假设四点共面,由共面向量定理得,存在实数x,y,使AD=xAB+yAC,即由①②得x=y=1,代入③式不成立,矛盾.∴假设不成立,故四点不共面.5.已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若AE=AA1+xAB+yAD,则x,y的值分别为()A.x=1,y=1B.x=1,y=C.x=,y=D.x=,y=1解析:选C.如图,AE=AA1+A1E=AA1+A1C1=AA1+(AB+AD).二、填空题6.已知2a+b=(0,-5,10),c=(1,-2,-2),a·c=4,|b|=12,则以b,c为方向向量的两直线的夹角为________.解析:由题意得(2a+b)·c=0+10-20=-10.即2a·c+b·c=-10,又∵a·c=4,∴b·c=-18,∴cos〈b,c〉===-,∴〈b,c〉=120°,∴两直线的夹角为60°.答案:60°7.如图,已知长方体ABCD-A1B1C1D1中,AB=AA1=2,BC=3,M为AC1与CA1的交点,则M点的坐标为__________.解析:由长方体的几何性质得,M为AC1的中点,在所给的坐标系中,A(0,0,0),C1(2,3,2),∴中点M的坐标为(1,,1).答案:(1,,1)8.(2012·保定质检)如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF,则EF与平面A1B1CD的位置关系为________.解析:取AB=a,AD=b,AA1=c为基底,易得EF=-(a+b-c),而DB1=a+b-c,即EF∥DB1,故EF∥DB1,且EF⊄平面A1B1CD,DB1⊂平面A1B1CD,所以EF∥平面A1B1CD.答案:平行三、解答题9.已知向量b与向量a=(2,-1,2)共线,且满足a·b=18,(ka+b)⊥(ka-b),求向量b及k的值.解:∵a,b共线,∴存在实数λ,使b=λa,∴a·b=λa2=λ|a|2=λ[]2=18,解得λ=2.∴b=(4,-2,4).∵(ka+b)⊥(ka-b),∴(ka+b)·(ka-b)=0.∴(ka+2a)·(ka-2a)=0.∴(k2-4)|a|2=0.∴k=±2.10.如图,在长方体ABCD-A1B1C1D1中,O为AC的中点.(1)化简:A1O-AB-AD;(2)设E是棱DD1上的点,且DE=DD1,若EO=xAB+yAD+zAA1,试求x、y、z的值.解:(1)∵AB+AD=AC,∴A1O-AB-AD=A1O-(AB+AD)=A1O-AC=A1O-AO=A1A.(2)∵EO=ED+DO=D1D+DB=D1D+(DA+AB)=A1A+DA+AB=AB-AD-AA1,∴x=,y=-,z=-.11.如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上的点,且满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点为O.(1)试用基向量AB,AE,AD1表示向量OD1;(2)求异面直线OD1与AE所成角的余弦值;(3)判断平面D1AE与平面ABCE是否垂直?并说明理由.解:(1)∵AB∥CE,AB=CE=2,∴四边形ABCE是平行四边形,∴O为BE的中点.∴OD1=AD1-AO=AD1-(AB+AE)=AD1-AB-AE.(2)设异面直线OD1与AE所成的角为θ,则cosθ=|cos〈OD1,AE〉|=,∵OD1·AE=(AD1-AB-AE)·AE=AD1·AE-AB·AE-|AE|2=1××cos45°-×2××cos45°-×()2=-1,|OD1|==,∴cosθ=|=||=.故异面直线OD1与AE所成角的余弦值为.(3)平面D1AE⊥平面ABCE.证明如下:取AE的中点M,连接D1M,则D1M=AM-AD1=AE-AD1,∴D1M·AE=(AE-AD1)·AE=|AE|2-AD1·AE=×()2-1××cos45°=0.∴D1M⊥AE.∴D1M⊥AE.∵D1M·AB=(AE-AD1)·AB=AE·AB-AD1·AB=××2×cos45°-1×2×cos60°=0,∴D1M⊥AB,∴D1M⊥AB.又AE∩AB=A,AE、AB⊂平面ABCE,∴D1M⊥平面ABCE.∵D1M⊂平面D1AE,∴平面D1AE⊥平面ABCE.