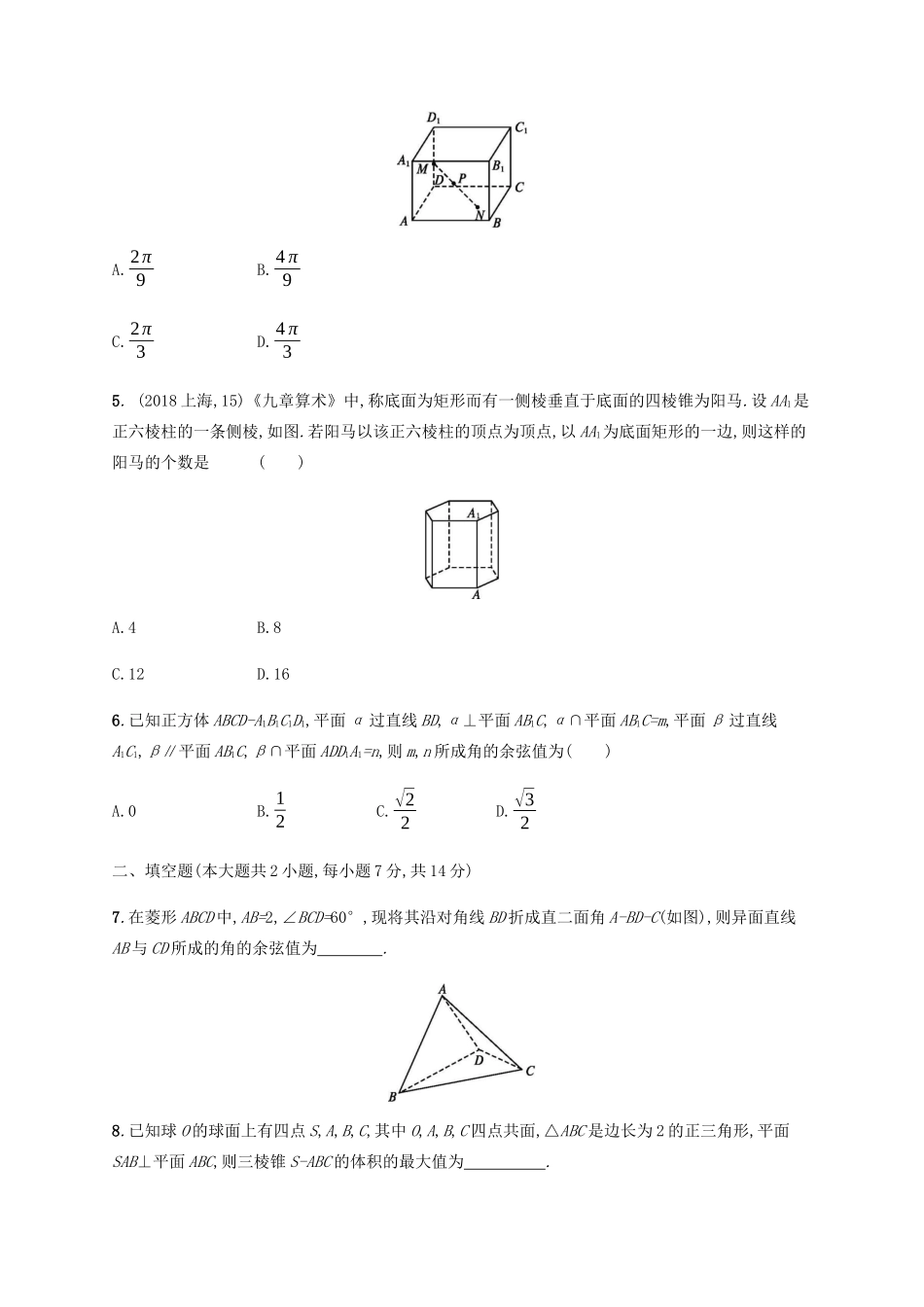
单元质检七立体几何(B)(时间:45分钟满分:100分)一、选择题(本大题共6小题,每小题7分,共42分)1.若圆锥的表面积是底面积的3倍,则该圆锥的侧面展开图扇形的圆心角为()A.2π3B.5π6C.πD.7π62.如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC的中点,则⃗AE·⃗BC等于()A.3B.2C.1D.03.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4.又H,G分别为BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形4.如图,已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共顶点D的三个面所围成的几何体的体积为()A.2π9B.4π9C.2π3D.4π35.(2018上海,15)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱,如图.若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马的个数是()A.4B.8C.12D.166.已知正方体ABCD-A1B1C1D1,平面α过直线BD,α⊥平面AB1C,α∩平面AB1C=m,平面β过直线A1C1,β∥平面AB1C,β∩平面ADD1A1=n,则m,n所成角的余弦值为()A.0B.12C.√22D.√32二、填空题(本大题共2小题,每小题7分,共14分)7.在菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成的角的余弦值为.8.已知球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则三棱锥S-ABC的体积的最大值为.三、解答题(本大题共3小题,共44分)9.(14分)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60°,AP=1,AD=√3,求三棱锥E-ACD的体积.10.(15分)如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.(1)求证:GF∥平面ADE;(2)求平面AEF与平面BEC所成锐二面角的余弦值.11.(15分)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=√2,BC=2√2,PA=2.(1)取PC的中点N,求证:DN∥平面PAB;(2)求直线AC与PD所成角的余弦值;(3)在线段PD上是否存在一点M,使得二面角M-AC-D的大小为45°?如果存在,求BM与平面MAC所成的角;如果不存在,请说明理由.单元质检七立体几何(B)1.C解析设圆锥的底面半径为r,母线长为l,侧面展开图扇形的圆心角为θ,根据条件得πrl+πr2=3πr2,即l=2r,根据扇形面积公式得θπl22π=πrl,即θ=r·2πl=r·2π2r=π,故选C.2.D解析⃗AE·⃗BC=(⃗AD+⃗DE)·⃗BC=⃗AD·⃗BC+⃗DE·⃗BC=⃗AD·(⃗BD+⃗DC)=⃗AD·⃗BD+⃗AD·⃗DC=0.3.B解析如图,由题意,得EF∥BD,且EF=15BD,HG∥BD,且HG=12BD,故EF∥HG,且EF≠HG.因此,四边形EFGH是梯形.由题可得EF∥平面BCD,而EH与平面ADC不平行,故选B.4.A解析MN=2,则DP=1,则点P的轨迹为以D为球心,半径r=1的球面的一部分,则球的体积为V=43π·r3=4π3. ∠BAD=60°,∴∠ADC=120°,120°为360°的13,只取半球的13,则V'=4π3×13×12=2π9.5.D解析设正六棱柱为ABCDEF-A1B1C1D1E1F1,以侧面AA1B1B,AA1F1F为底面矩形的阳马有E-AA1B1B,E1-AA1B1B,D-AA1B1B,D1-AA1B1B,C-AA1F1F,C1-AA1F1F,D-AA1F1F,D1-AA1F1F,共8个;以对角面AA1C1C,AA1E1E为底面矩形的阳马有F-AA1C1C,F1-AA1C1C,D-AA1C1C,D1-AA1C1C,B-AA1E1E,B1-AA1E1E,D-AA1E1E,D1-AA1E1E,共8个.所以共有8+8=16(个),故选D.6.D解析如图所示, BD1⊥平面AB1C,平面α过直线BD,α⊥平面AB1C,∴平面α即为平面DBB1D1.设AC∩BD=O.∴α∩平面AB1C=OB1=m. 平面A1C1D过直线A1C1,与平面AB1C平行,而平面β过直线A1C1,β∥平面AB1C,∴平面A1C1D即为平面β.β∩平面ADD1A1=A1D=n,又A1D∥B1C,∴m,n所成角为∠OB1C,由△AB1C为正三角形,则cos∠OB1C=cosπ6=√32.故选D.7.14解析如图,取BD的中点O,连接AO,CO,建立如图所示的空间直角坐标系, AB=2,∠BCD=60°,∴A(0,0,√3),B(1,0,0),D(-1,0,0),C(0,√3,0),∴⃗AB=(1,0,-√3),⃗CD=(-1,-√3,0),∴cos<⃗AB,⃗CD>=⃗AB·⃗CD|⃗AB...