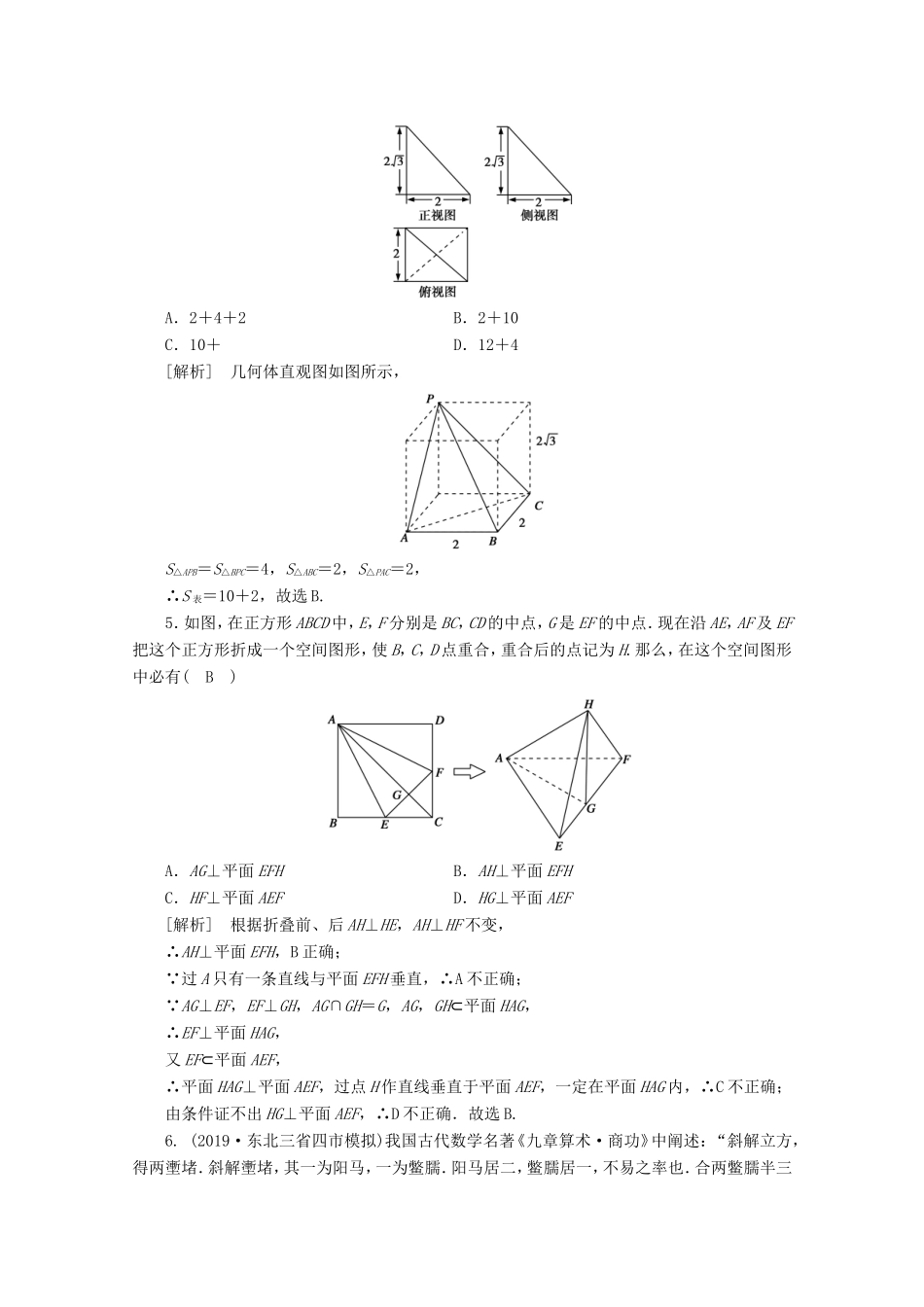
[考案7]第七章综合过关规范限时检测(时间:120分钟满分150分)一、单选题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中只有一个是符合题目要求的)1.(2020·河北省衡水中学调研)下列命题正确的个数为(C)①梯形一定是平面图形;②若两条直线和第三条直线所成的角相等,则这两条直线平行;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.A.0B.1C.2D.3[解析]①由于梯形是有一组对边平行的四边形,易知两平行线确定一平面,所以梯形可以确定一个平面,故①对;②若两条直线和第三条直线所成的角相等,比如等腰三角形ABC,AB=AC,直线AB,AC与直线BC所成的角相等,而直线AB,AC不平行,故②错;③两两相交的三条直线,比如墙角处的三条交线可以确定三个平面,故③对;④如果两个平面有三个公共点,比如两平面相交有一条公共直线,如果这三个公共点不共线,则这两个平面重合,故④错.综上,选C.2.(2019·黑龙江哈师大附中期中)若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法中正确的是(C)A.α∥β,m⊂α,n⊂β⇒m∥nB.α⊥γ,β⊥γ⇒α∥βC.α∥β,m∥n,m⊥α⇒n⊥βD.α∩β=m,β∩γ=n,m∥n⇒α∥β[解析]对于A.α∥β,m⊂α,n⊂β⇒m∥n,错误;m与n又有可能异面;对于B.α⊥γ,β⊥γ⇒α∥β,错误,α与β有可能相交;对于C.α∥β,m∥n,m⊥α⇒n⊥β,利用直线与平面垂直的判定定理可得结论正确;对于D.α∩β=m,β∩γ=n,m∥n⇒α∥β,错误,α与β有可能相交.故选C.3.(2019·全国Ⅱ)设α,β为两个平面,则α∥β的充要条件是(B)A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面[解析]由面面平行的判定定理知:α内两条直交直线都与β平行是α∥β的充分条件,由面面平行性质定理知,若α∥β,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是α∥β的必要条件,故选B.4.(2019·江西吉安五校联考)某几何体的三视图如图所示,则该几何体的表面积为(B)A.2+4+2B.2+10C.10+D.12+4[解析]几何体直观图如图所示,S△APB=S△BPC=4,S△ABC=2,S△PAC=2,∴S表=10+2,故选B.5.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D点重合,重合后的点记为H.那么,在这个空间图形中必有(B)A.AG⊥平面EFHB.AH⊥平面EFHC.HF⊥平面AEFD.HG⊥平面AEF[解析]根据折叠前、后AH⊥HE,AH⊥HF不变,∴AH⊥平面EFH,B正确; 过A只有一条直线与平面EFH垂直,∴A不正确; AG⊥EF,EF⊥GH,AG∩GH=G,AG,GH⊂平面HAG,∴EF⊥平面HAG,又EF⊂平面AEF,∴平面HAG⊥平面AEF,过点H作直线垂直于平面AEF,一定在平面HAG内,∴C不正确;由条件证不出HG⊥平面AEF,∴D不正确.故选B.6.(2019·东北三省四市模拟)我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑半三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:①四个侧面都是直角三角形;②最长的侧棱长为2;③四个侧面中有三个侧面是全等的直角三角形;④外接球的表面积为24π.其中正确的个数为(D)A.0B.1C.2D.3[解析]由三视图可知,该几何体为四棱锥P-ABCD,四边形ABCD为矩形,AB=4,AD=2,PD⊥平面ABCD,PD=2,对于①易证AB⊥平面PAD,BC⊥平面PCD,故四个侧面都是直角三角形;对于②PB==2,故正确;对于③四个侧面中没有全等的三角形,故错误;对于④外接球的直径为PB=2,故外接球的表面积为24π,正确,故选D.7.(2019·上饶模拟)已知正三棱柱ABC-A1B1C1,AB=AA1=2,则异面直线AB1与CA1所成角的余弦值为(C)A.0B.-C.D.[解析]如图,将三棱柱补成四棱柱,连D1C,则D1C∥AB1,∴∠D1CA1即为异面直线AB1,CA1所成的角θ,由题意知CD1=CA1=2,D1A1=2,∴cosθ==...