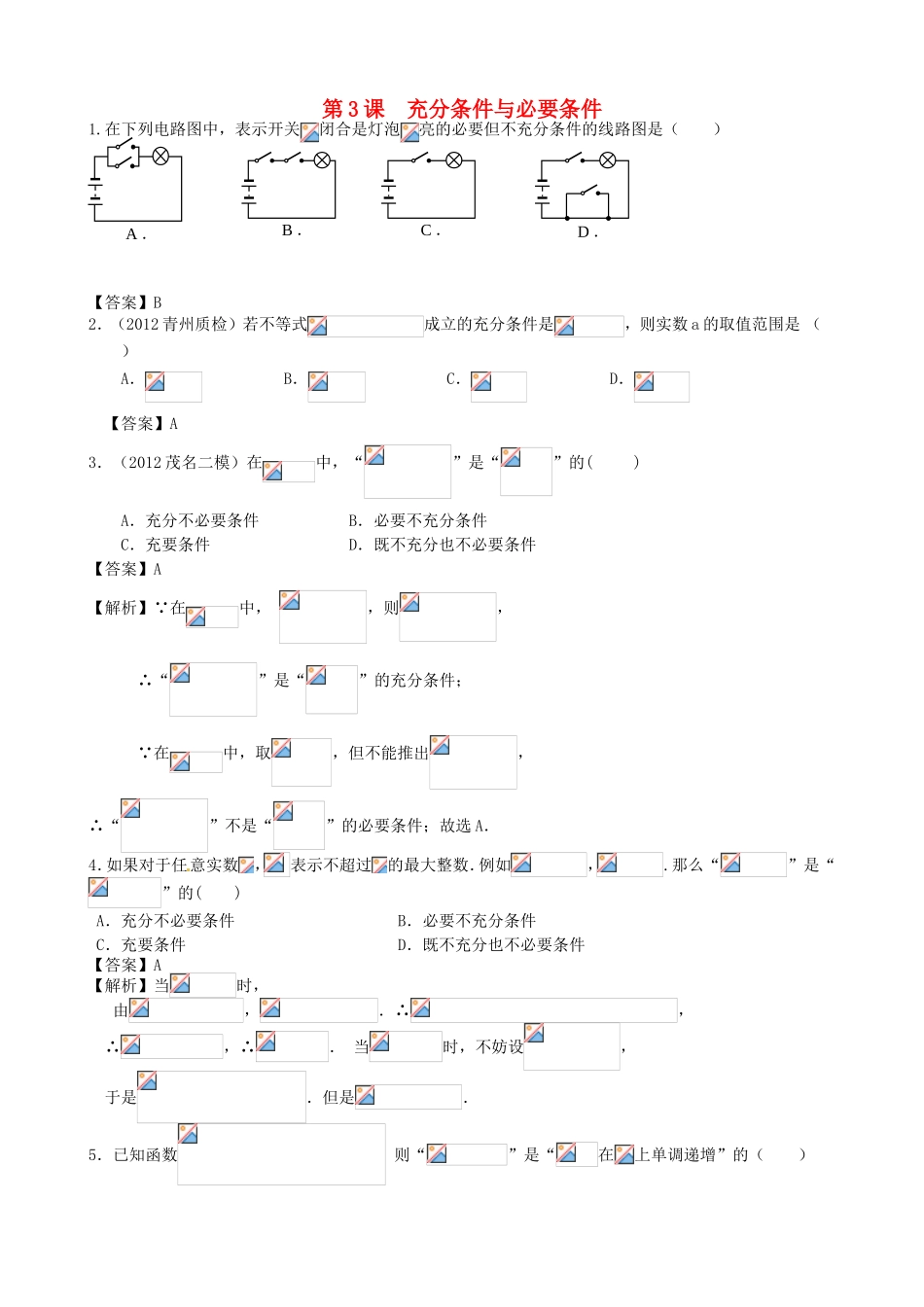
第3课充分条件与必要条件1.在下列电路图中,表示开关闭合是灯泡亮的必要但不充分条件的线路图是()【答案】B2.(2012青州质检)若不等式成立的充分条件是,则实数a的取值范围是()A.B.C.D.【答案】A3.(2012茂名二模)在中,“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】∵在中,,则,∴“”是“”的充分条件;∵在中,取,但不能推出,∴“”不是“”的必要条件;故选A.4.如果对于任意实数,表示不超过的最大整数.例如,.那么“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】当时,由,.∴,∴,∴.当时,不妨设,于是.但是.5.已知函数则“”是“在上单调递增”的()A.B.C.D.A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】当时,,在上单调递增.当时,,解得,∴在上单调递增时的取值范围是,故选B.6.(2012福建高考)下列命题中,真命题是()A.B.C.的充要条件是D.是的充分条件【答案】D.【解析】∵对任意恒成立,∴A错误;∵当时,,,∴B错误;∵当时,而无意义,∴C错误.7.探求关于的方程两根都大于的充要条件.【解析】设两根为,,则,∴方程两根都大于2的充要条件为.8.(2012日照质检)设命题:实数满足,其中,命题:实数满足.(1)若,且为真,求实数的取值范围;(2)若是的必要不充分条件,求实数的取值范围.【解析】(1)时,:,即:,:,∴,即:.由为真知,.(2)由,得,若,则,不合题意;若,则,由题意知,,∴,∴.