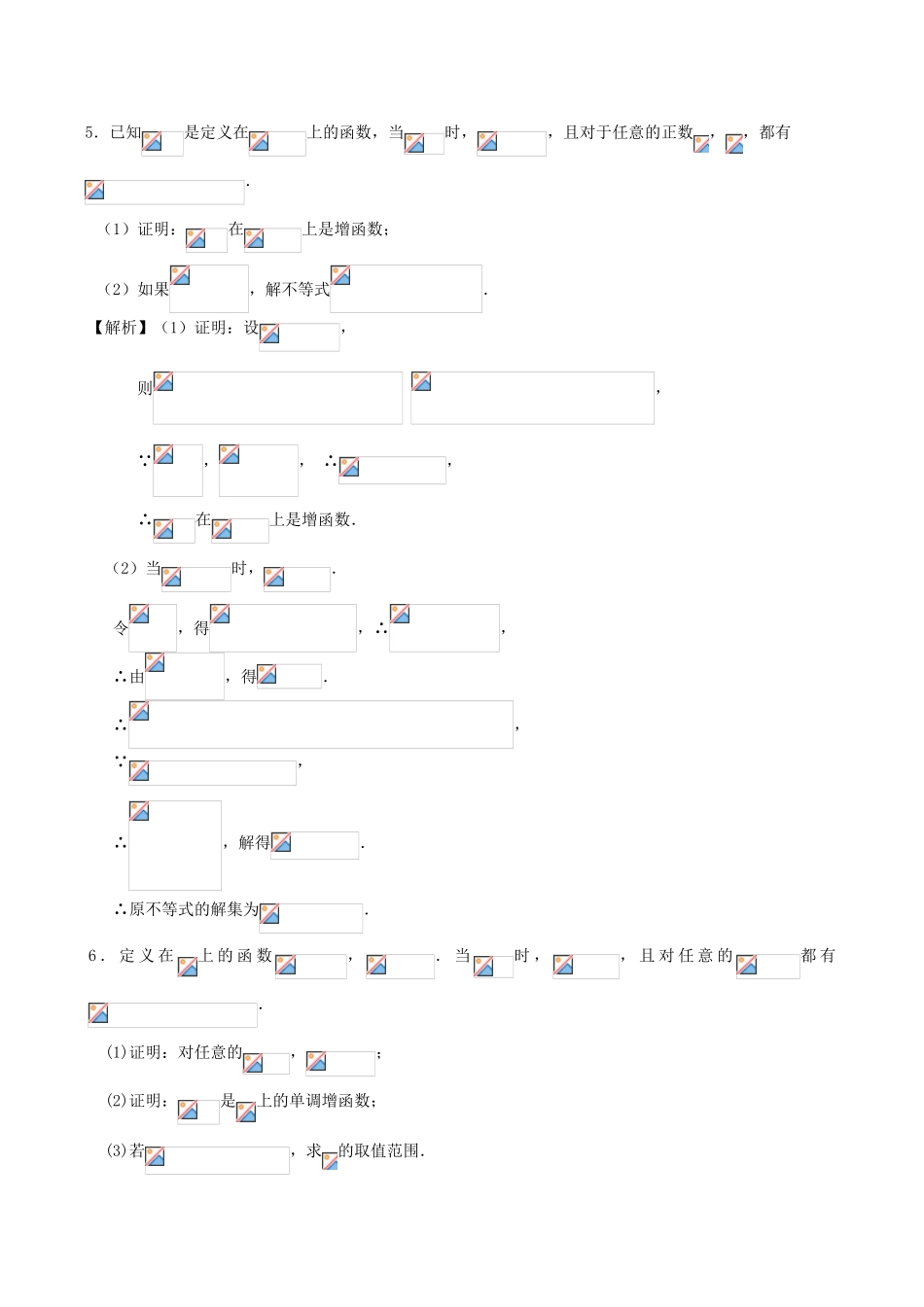
第19课抽象函数1.(2012汕头质检)已知函数是定义在上的奇函数,若对于任意给定的不等实数、,不等式恒成立,则不等式的解集为()A.B.C.D.【答案】B【解析】是奇函数,∴的图象关于点对称,∵恒成立,∴为上的减函数;∵,∴,∴,∴.2.(2012湛江二模)对一个定义在上的函数有以下四种说法:①,;②在区间上单调递减;③对任意满足;④是奇函数.则以上说法中能同时成立的最多有()A.1个B.2个C.3个D.4个【答案】B【解析】②③,②④,③④都可以同时成立.3.(2012聊城质检)已知定义在上的函数满足下列三个条件:①对于任意的都有;②对于任意的都有;③函数的图象关于轴对称.则下列结论正确的是()A.B.C.D.【答案】C【解析】∵,∴,,,∵函数的图象关于轴对称,∴,∴,,∵对于任意的都有;∴4.已知,、,且对任意、都有:①,②.给出以下三个结论:(1),(2),(3).其中正确的个数为()A.B.C.D.【答案】A【解析】由①,得.②,∴,∴.∴,,.5.已知是定义在上的函数,当时,,且对于任意的正数,,都有.(1)证明:在上是增函数;(2)如果,解不等式.【解析】(1)证明:设,则,∵,,∴,∴在上是增函数.(2)当时,.令,得,∴,∴由,得.∴,∵,∴,解得.∴原不等式的解集为.6.定义在上的函数,.当时,,且对任意的都有.(1)证明:对任意的,;(2)证明:是上的单调增函数;(3)若,求的取值范围.【解析】(1)证明:令,得,∵,∴.令,则,∴,设,则,,∴.(2)证明:设,则.∵,∴,且,∴,∴是上的单调增函数.(3)由,得,解得.∴的取值范围是.