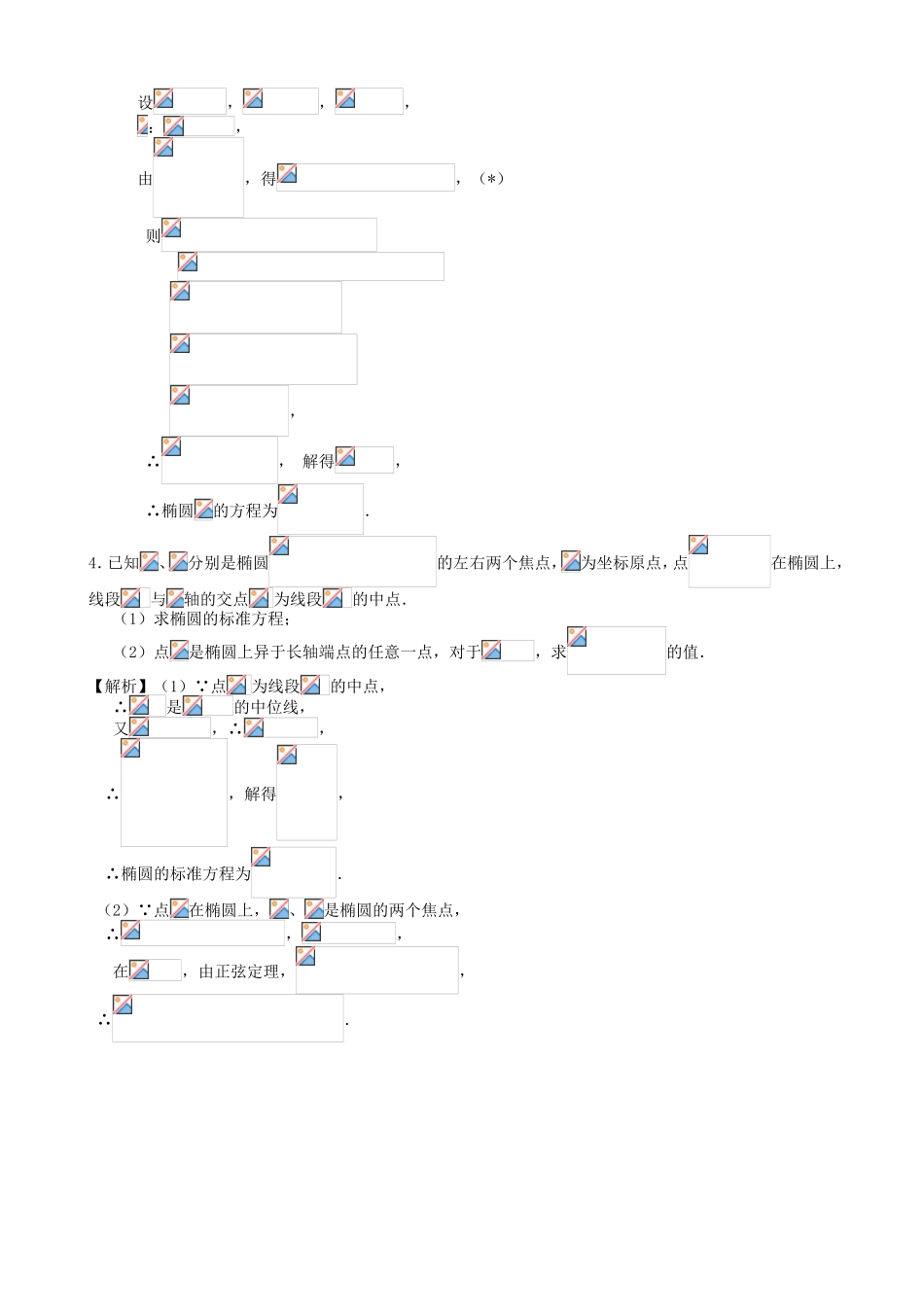
第十章圆锥曲线第63课椭圆及其标准方程1.(2012哈尔滨质检)设、分别是椭圆的左、右焦点,是第一象限内该椭圆上的一点,且,求点的横坐标为()A.1B.C.D.【答案】D【解析】∵,∴,,设,∵,∴,即,∴.又∵,∴,解得,∵,∴.∵,∴.2.(2012莱芜质检)若点和点分别为椭圆的中心和左焦点,点为椭圆上任意一点,则最小值为()A.B.C.D.【答案】A【解析】由已知可得,设,则,∵,∴时,取得最小值.3.(2012上海闸北质检)椭圆的左、右焦点分别是,,过的直线与椭圆相交于,两点,且,,成等差数列.(1)求证:;(2)若直线的斜率为1,且点在椭圆上,求椭圆的方程.【解析】(1)由题设,得,由椭圆定义,∴.(2)由点在椭圆上,可设椭圆的方程为,设,,,:,由,得,(*)则,∴,解得,∴椭圆的方程为.4.已知、分别是椭圆的左右两个焦点,为坐标原点,点在椭圆上,线段与轴的交点为线段的中点.(1)求椭圆的标准方程;(2)点是椭圆上异于长轴端点的任意一点,对于,求的值.【解析】(1)∵点为线段的中点,∴是的中位线,又,∴,∴,解得,∴椭圆的标准方程为.(2)∵点在椭圆上,、是椭圆的两个焦点,∴,,在,由正弦定理,,∴.5.(2012北京石景山一模)已知椭圆()右顶点到右焦点的距离为,短轴长为.(1)求椭圆的方程;(2)过左焦点的直线与椭圆分别交于、两点,若线段的长为,求直线的方程.【解析】(1)由题意得,解得.∴椭圆方程为.(2)当直线与轴垂直时,,此时不符合题意故舍掉;当直线与轴不垂直时,设直线的方程为:,由,得.设,则,∴,由,∴直线,或.6.(2013揭阳联考)如图,在中,,,以、为焦点的椭圆恰好过的中点.(1)求椭圆的标准方程;(2)过椭圆的右顶点作直线与圆相交于、两点,试探究点、能将圆分割成弧长比值为的两段弧吗?若能,求出直线的方程;若不能,请说明理由.【解析】(1)∵,∴,∴,∴,∴,,∴,∴,又,∴,∴椭圆的标准方程为(2)椭圆的右顶点,圆圆心为,半径.假设点、能将圆分割成弧长比值为的两段弧,则,圆心到直线的距离.当直线斜率不存在时,的方程为,此时圆心到直线的距离(符合),当直线斜率存在时,设的方程为,即,∴圆心到直线的距离,无解.综上:点M、N能将圆分割成弧长比值为的两段弧,此时方程为.POCyxBA