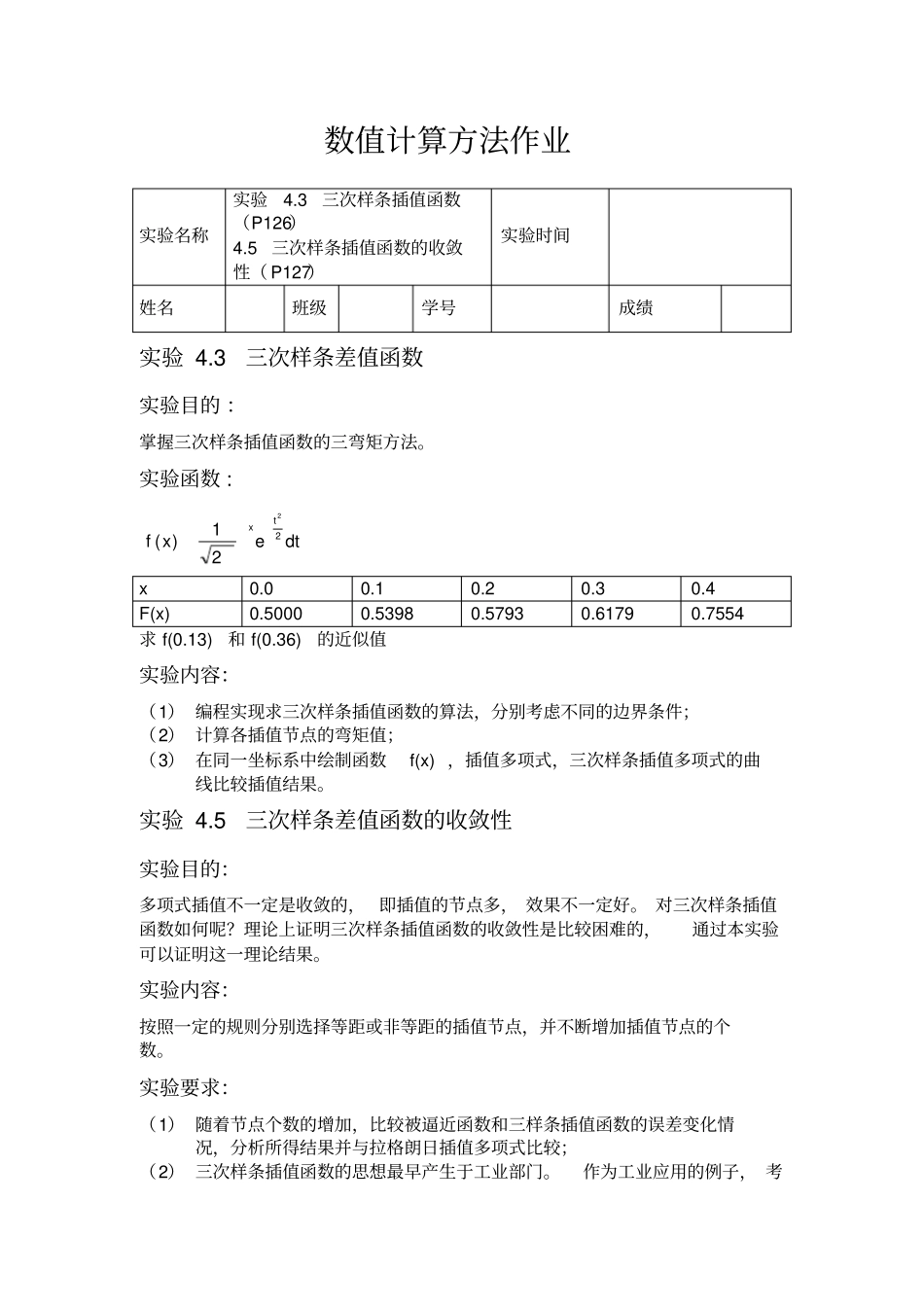
数值计算方法作业实验4.3三次样条差值函数实验目的:掌握三次样条插值函数的三弯矩方法。实验函数:dtexfxt2221)(x0.00.10.20.30.4F(x)0.50000.53980.57930.61790.7554求f(0.13)和f(0.36)的近似值实验内容:(1)编程实现求三次样条插值函数的算法,分别考虑不同的边界条件;(2)计算各插值节点的弯矩值;(3)在同一坐标系中绘制函数f(x),插值多项式,三次样条插值多项式的曲线比较插值结果。实验4.5三次样条差值函数的收敛性实验目的:多项式插值不一定是收敛的,即插值的节点多,效果不一定好。对三次样条插值函数如何呢?理论上证明三次样条插值函数的收敛性是比较困难的,通过本实验可以证明这一理论结果。实验内容:按照一定的规则分别选择等距或非等距的插值节点,并不断增加插值节点的个数。实验要求:(1)随着节点个数的增加,比较被逼近函数和三样条插值函数的误差变化情况,分析所得结果并与拉格朗日插值多项式比较;(2)三次样条插值函数的思想最早产生于工业部门。作为工业应用的例子,考实验名称实验4.3三次样条插值函数(P126)4.5三次样条插值函数的收敛性(P127)实验时间姓名班级学号成绩虑如下例子:某汽车制造商根据三次样条插值函数设计车门曲线,其中一段数据如下:kx012345678910ky0.00.791.532.192.713.033.272.893.063.193.29ky0.80.2算法描述:拉格朗日插值:其中是拉格朗日基函数,其表达式为:nijjjijixxxxxl0)()(牛顿插值:))...()(](,...,,[....))(0](,,[)0](,[)()(1102101210100nnnxxxxxxxxxxfxxxxxxxfxxxxfxfxN其中)/(]),...,[],...,[(]...,[..],[],[],,[)()(],[01102110xxxxxfxxxfxxxfxxxxfxxfxxxfxxxfxfxxfnnnnikjikjkjijijiji三样条插值:所谓三次样条插值多项式Sn(x)是一种分段函数,它在节点Xi(a=jY(i)=(Y(i)-Y(i-1))/(X(i)-X(i-j+1));elseY(i)=0;endendnewt=[newt,Y'];end%计算牛顿插值f=newt(1,2);fori=2:nz=1;fork=1:i-1z=(xi-X(k))*z;endf=f+newt(i-1,i)*z;endfprintf('%d\n',f)return3三次样条插值第一类边界条件Threch.mfunctionS=Threch1(X,Y,dy0,dyn,xi)%X为已知数据的横坐标%Y为已知数据的纵坐标%xi插值点处的横坐标%S...