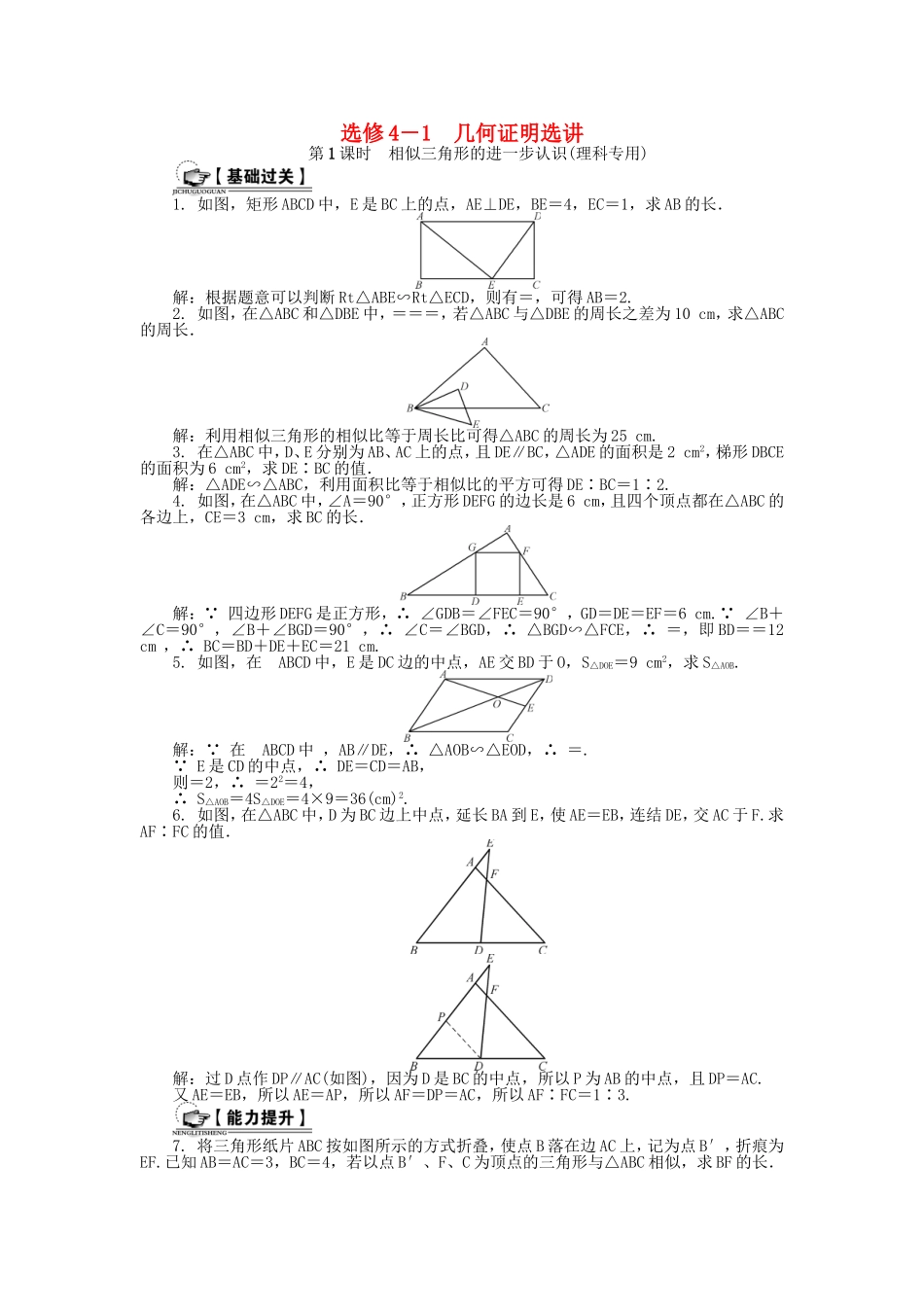
选修4-1几何证明选讲第1课时相似三角形的进一步认识(理科专用)1.如图,矩形ABCD中,E是BC上的点,AE⊥DE,BE=4,EC=1,求AB的长.解:根据题意可以判断Rt△ABE∽Rt△ECD,则有=,可得AB=2.2.如图,在△ABC和△DBE中,===,若△ABC与△DBE的周长之差为10cm,求△ABC的周长.解:利用相似三角形的相似比等于周长比可得△ABC的周长为25cm.3.在△ABC中,D、E分别为AB、AC上的点,且DE∥BC,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,求DE∶BC的值.解:△ADE∽△ABC,利用面积比等于相似比的平方可得DE∶BC=1∶2.4.如图,在△ABC中,∠A=90°,正方形DEFG的边长是6cm,且四个顶点都在△ABC的各边上,CE=3cm,求BC的长.解: 四边形DEFG是正方形,∴∠GDB=∠FEC=90°,GD=DE=EF=6cm. ∠B+∠C=90°,∠B+∠BGD=90°,∴∠C=∠BGD,∴△BGD∽△FCE,∴=,即BD==12cm,∴BC=BD+DE+EC=21cm.5.如图,在ABCD中,E是DC边的中点,AE交BD于O,S△DOE=9cm2,求S△AOB.解: 在ABCD中,AB∥DE,∴△AOB∽△EOD,∴=. E是CD的中点,∴DE=CD=AB,则=2,∴=22=4,∴S△AOB=4S△DOE=4×9=36(cm)2.6.如图,在△ABC中,D为BC边上中点,延长BA到E,使AE=EB,连结DE,交AC于F.求AF∶FC的值.解:过D点作DP∥AC(如图),因为D是BC的中点,所以P为AB的中点,且DP=AC.又AE=EB,所以AE=AP,所以AF=DP=AC,所以AF∶FC=1∶3.7.将三角形纸片ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角形与△ABC相似,求BF的长.解:设BF=x.若△CFB′∽△CBA,则=,即=.∴12-3x=4x,∴x=.若△CFB′∽△CAB,则=,即=,得x=2.即BF=2或.8.如图,在△ABC中,D是AC中点,E是BD三等分点,AE的延长线交BC于F.求的值.解:过D点作DM∥AF交BC于M.因为DM∥AF,所以==.因为EF∥DM,所以=,即S△BDM=9S△BEF.又=,即S△DMC=S△BDM=6S△BEF,所以S四边形DEFC=14S△BEF,因此=.9.如图所示,在△ABC中,AD为BC边上的中线,F为AB上任意一点,CF交AD于点E.求证:AE·BF=2DE·AF.证明:过点D作AB的平行线DM交AC于点M,交FC于点N.在△BCF中,D是BC的中点,DN∥BF,∴DN=BF. DN∥AF,∴△AFE∽△DNE.∴=. DN=BF,∴=,即AE·BF=2DE·AF.10.如图,在△ABC中,AB=AC,延长BC到D,使CD=BC,CE⊥BD,交AD于E,连结BE,交AC于点F.求证:AF=FC.证明:取BC的中点H,连结AH. AB=AC,∴AH⊥BC. CE⊥BD,∴AH∥EC. CD=BC,∴CD=2CH.则DE=2AE.取ED的中点M,连结CM.则ME=AE. C为BD的中点,∴CM∥BE.则F为AC的中点,即AF=FC.11.如图,AB是圆O的直径,弦BD、CA的延长线相交于点E,EF垂直BA,交BA的延长线于点F.(1)求证:∠DEA=∠DFA;(2)若∠EBA=30°,EF=,EA=2AC,求AF的长.(1)证明:连结AD、BC.因为AB是圆O的直径,所以∠ADB=∠ACB=∠EFA=90°,故A、D、E、F四点共圆,所以∠DEA=∠DFA.(2)解:在Rt△EFA和Rt△BCA中,∠EAF=∠CAB,所以△EFA∽△BCA,故=.设AF=a,又EF=,∠EBA=30°,所以BF=3,则AB=3-a,AE2=AF2+EF2=a2+3.所以a(3-a)=(3+a2),解得a=1.所以AF的长为1.第2课时圆的进一步认识(理科专用)1.(2014·南京、盐城期末)如图,AB、CD是半径为1的圆O的两条弦,它们相交于AB的中点P,若PC=,OP=,求PD的长.解:因为P为AB中点,所以OP⊥AB,所以PB==.因为PC·PD=PA·PB=PB2=,由PC=,得PD=.2.如图,圆O上一点C在直径AB上的射影为D,点D在半径OC上的射影为E.若AB=3AD,求的值.解:设圆的半径为R,则AD==R,OD=R-R=R.又OD2=OE·OC,所以OE==R,CE=R-R=R,所以=8.3.如图,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D.若PA=3,PD∶DB=9∶16,分别求PD、AB的值.解:由PD∶DB=9∶16,可设PD=9x,DB=16x.因为PA为圆O的切线,所以PA2=PD·PB,所以32=9x·(9x+16x),化为x2=,所以x=.所以PD=9x=,PB=25x=5.因为AB为圆O的直径,PA为圆O的切线,所以AB⊥PA.所以AB===4.4.(2014·苏北三市期末)如图,锐角△ABC的内心为D,过...