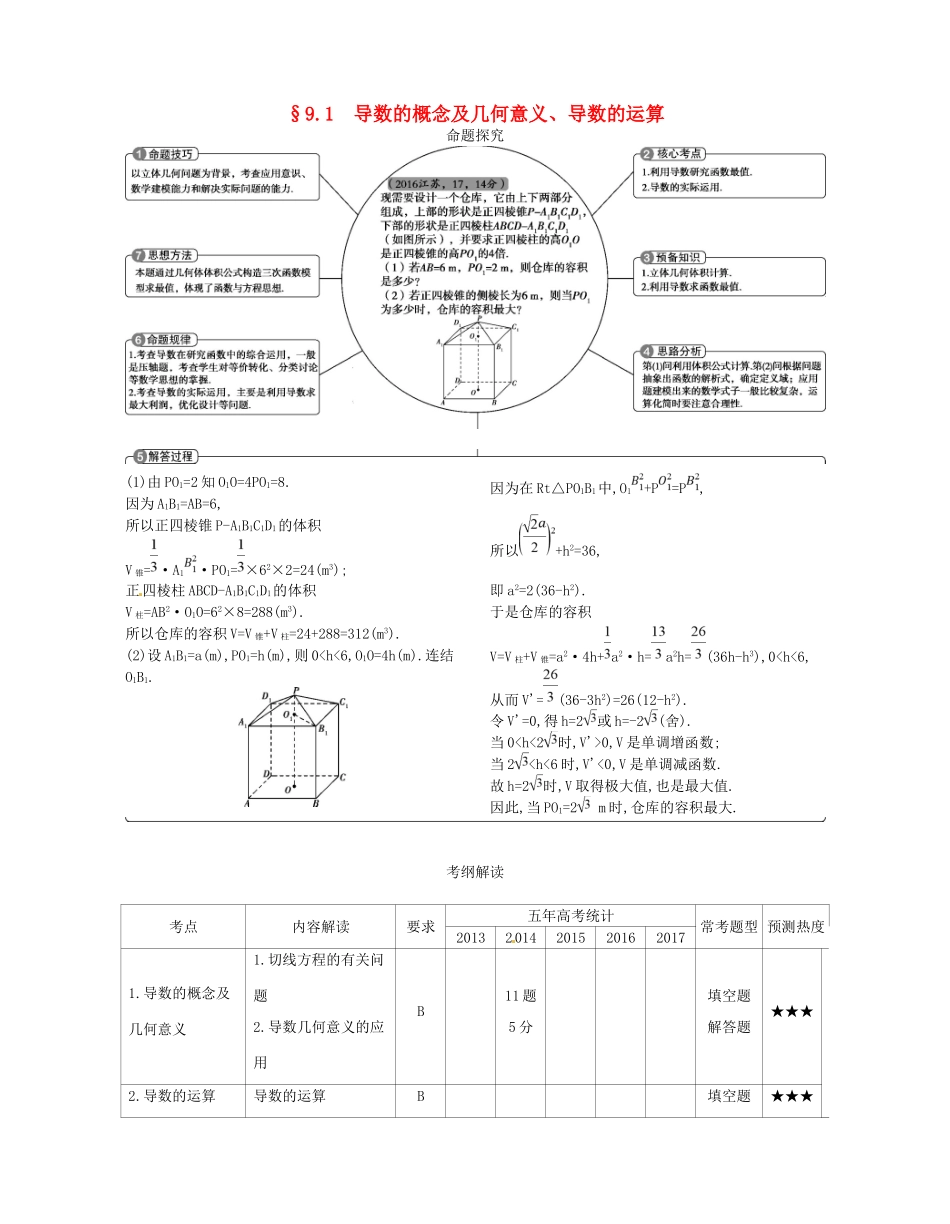
§9.1导数的概念及几何意义、导数的运算命题探究(1)由PO1=2知O1O=4PO1=8.因为A1B1=AB=6,所以正四棱锥P-A1B1C1D1的体积V锥=·A1·PO1=×62×2=24(m3);正四棱柱ABCD-A1B1C1D1的体积V柱=AB2·O1O=62×8=288(m3).所以仓库的容积V=V锥+V柱=24+288=312(m3).(2)设A1B1=a(m),PO1=h(m),则00,V是单调增函数;当20)上点P处的切线垂直,则P的坐标为.答案(1,1)5.(2014江苏,11,5分)在平面直角坐标系xOy中,若曲线y=ax2+(a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是.答案-3教师用书专用(6—9)6.(2013广东理,10,5分)若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=.答案-17.(2013重庆理,17,13分)设f(x)=a(x-5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).(1)确定a的值;(2)求函数f(x)的单调区间与极值.解析(1)因f(x)=a(x-5)2+6lnx,故f'(x)=2a(x-5)+.令x=1,得f(1)=16a,f'(1)=6-8a,所以曲线y=f(x)在点(1,f(1))处的切线方程为y-16a=(6-8a)(x-1),由点(0,6)在切线上可得6-16a=8a-6,故a=.(2)由(1)知,f(x)=(x-5)2+6lnx(x>0),f'(x)=x-5+=.令f'(x)=0,解得x1=2,x2=3.当03时,f'(x)>0,故f(x)在(0,2),(3,+∞)上为增函数;当22;(3)设实数k使得f(x)>k对x∈(0,1)恒成立,求k的最大值.解析(1)因为f(x)=ln(1+x)-ln(1-x),所以f'(x)=+,f'(0)=2.又因为f(0)=0,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=2x.(2)证明:令g(x)=f(x)-2,则g'(x)=f'(x)-2(1+x2)=.因为g'(x)>0(0g(0)=0,x∈(0,1),即当x∈(0,1)时,f(x)>2.(3)由(2)知,当k≤2时,f(x)>k对x∈(0,1)恒成立.当k>2时,令h(x)=f(x)-k,则h'(x)=f'(x)-k(1+x2)=.所以当02时,f(x)>k并非对x∈(0,1)恒成立.综上可知,k的最大值为2.9.(2013北京理,18,13分)设L为曲线C:y=在点(1,0)处的切线.(1)求L的方程;(2)证明:除切点(1,0)之外,曲线C在直线L的下方.解析(1)设f(x)=,则f'(x)=.所以f'(1)=1.所以L的方程为y=x-1.(2)证明:令g(x)=x-1-f(x),则除切点之外,曲线C在直线L的下方等价于g(x)>0(x>0,x≠1).g(x)∀满足g(1)=0,且g'(x)=1-f'(x)=.当01时,x2-1>0,lnx>0,所以g'(x)>0,故g(x)单调递增.所以,g(x)>g(1)=0(x>0,x≠1).∀所以除切点之外,曲线C在直线L的下方.考点二导数的运算1.(2016天津,10,5分)已知函数f(x)=(2x+1)ex,f'(x)为f(x)的导函数,则f'(0)的值为.答案32.(2014福建,20,14分)已知函数f(x)=ex-ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为-1.(1)求...