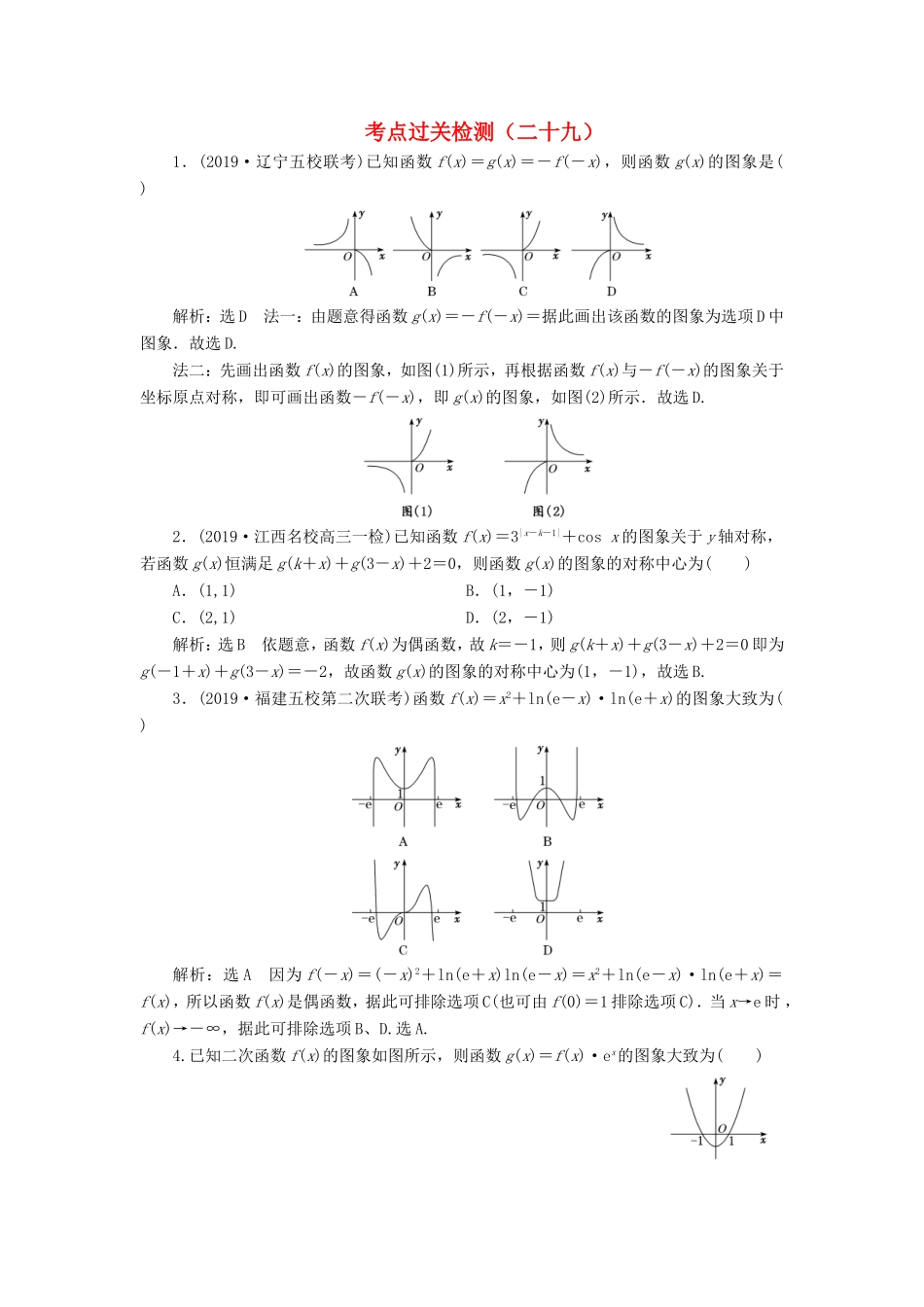
考点过关检测(二十九)1.(2019·辽宁五校联考)已知函数f(x)=g(x)=-f(-x),则函数g(x)的图象是()解析:选D法一:由题意得函数g(x)=-f(-x)=据此画出该函数的图象为选项D中图象.故选D.法二:先画出函数f(x)的图象,如图(1)所示,再根据函数f(x)与-f(-x)的图象关于坐标原点对称,即可画出函数-f(-x),即g(x)的图象,如图(2)所示.故选D.2.(2019·江西名校高三一检)已知函数f(x)=3|x-k-1|+cosx的图象关于y轴对称,若函数g(x)恒满足g(k+x)+g(3-x)+2=0,则函数g(x)的图象的对称中心为()A.(1,1)B.(1,-1)C.(2,1)D.(2,-1)解析:选B依题意,函数f(x)为偶函数,故k=-1,则g(k+x)+g(3-x)+2=0即为g(-1+x)+g(3-x)=-2,故函数g(x)的图象的对称中心为(1,-1),故选B.3.(2019·福建五校第二次联考)函数f(x)=x2+ln(e-x)·ln(e+x)的图象大致为()解析:选A因为f(-x)=(-x)2+ln(e+x)ln(e-x)=x2+ln(e-x)·ln(e+x)=f(x),所以函数f(x)是偶函数,据此可排除选项C(也可由f(0)=1排除选项C).当x→e时,f(x)→-∞,据此可排除选项B、D.选A.4.已知二次函数f(x)的图象如图所示,则函数g(x)=f(x)·ex的图象大致为()解析:选A由图象知,当x<-1或x>1时,f(x)>0;当-10恒成立,结合选项可知选A.5.(2019·合肥九中模拟)现有四个函数:①y=x·sinx,②y=x·cosx,③y=x·|cosx|,④y=x·2x的部分图象如图,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是()A.①④②③B.①④③②C.④①②③D.③④②①解析:选A函数①y=x·sinx为偶函数,图象关于y轴对称,对应的是第一个函数图象,从而排除选项C、D;对于函数④y=x·2x,因为y′=2x(1+xln2),当x>0时,y′>0,函数单调递增,所以函数④y=x·2x对应的是第二个函数图象;又当x>0时,函数③y=x·|cosx|≥0,对应的是第四个函数图象,从而排除选项B,选A.6.(2019·广州七校第二次联考)设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的部分图象大致为()解析:选B因为f′(x)=sinx+xcosx-sinx=xcosx,所以k=g(t)=f′(t)=tcost.因为g(-t)=-tcos(-t)=-tcost=-g(t),所以函数g(t)是奇函数,所以其图象关于原点对称,排除A、C;又当t∈时,g(t)>0,排除D,故选B.7.(2019·兰州模拟)如图,四棱锥PABCD的底面是边长为2的正方形,PA⊥平面ABCD,且PA=4,M是PB上(P,B点除外)的一个动点,过点M作平面α∥平面PAD,截棱锥所得截面面积为y,若平面α与平面PAD之间的距离为x,则函数y=f(x)的大致图象是()解析:选D法一:过点M作MT∥PA交AB于点T,过点M作MN∥BC交PC于点N,过点N作NS∥PD交CD于点S,连接TS(如图所示),则平面MTSN∥平面PAD,所以y=S四边形MTSN.由PA⊥平面ABCD,可得MT⊥平面ABCD,所以平面α与平面PAD之间的距离为x=AT,且四边形MTSN为直角梯形.由MT∥PA,MN∥BC,得=,=,所以MT=×4=2(2-x),MN=×2=x,所以y=S四边形MTSN=(MN+ST)=(2-x)(x+2)=4-x2(0