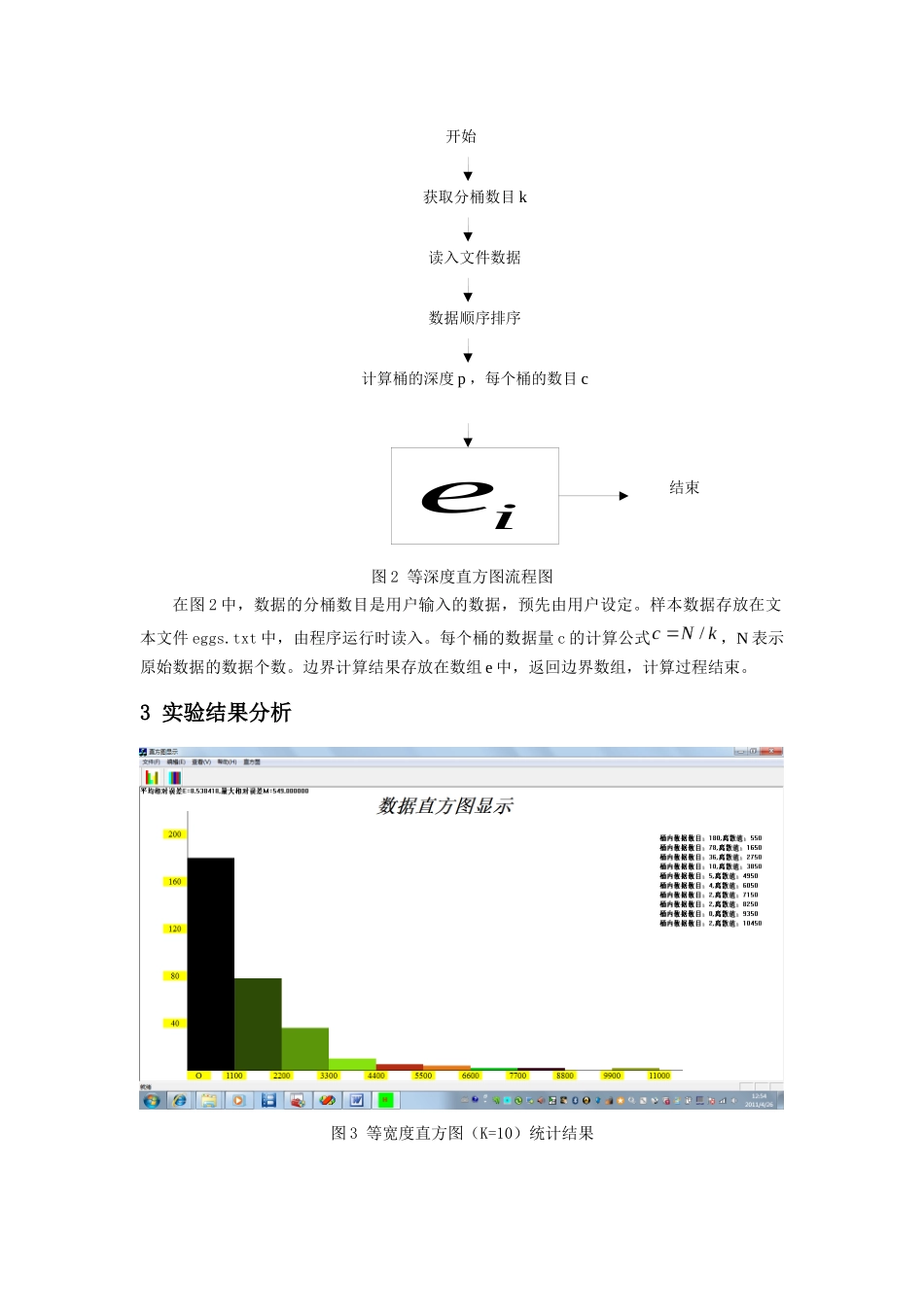
实验题目:直方图进行数据离散化1实验目的直方图使用分箱来近似数据分布,是数据规约的一种形式。通过本实验,需要掌握不同直方图的数学原理和构造方法。同时,掌握使用不同直方图对数据进行离散化的原理和方法。最后,利用实验数据实现一种直方图并进行评估。2实验步骤2.1算法原理首先,假设有N个自然数的集合U={x|x∈N},其中最大值为。(1)等宽度直方图对数据进行分箱。假设按等宽度的方法进行分箱(宽度w=1),则对于N个数据,按其值分别放入到相应的箱中,箱子的数目。设每个箱中的统计数据为,按照坐标值/频率对()表示在二维坐标上,则可以得到该组数据的单桶直方图。其中,。一般情况下,为了进一步压缩数据,通常进行数据分箱时,每一个桶代表的是连续的属性值,即取宽度。在这种分箱方法下,分箱数目。则按照公式,其中,令所得到的值/频率对,的宽度为q的直方图,即为常见的等宽度直方图。(2)等深度直方图与等宽度直方图相比,等深度直方图仅仅是在创建数据桶时与其不同。等深度直方图的数据桶的创建思想是:使得每个桶的频率粗略的为常数,即每个桶中包含大致相当的样本数据数目。设分箱的数目为K,则对于每一个桶,有,其中。只有在这种情况下,才满足大致相当。所要求的是每一个桶的边界,开始获取分桶数目k读入文件数据计算桶宽度w逐个扫描数据,统计数目结束。求边界的过程:首先对该集合U进行排序(由小到大),由于每桶的数目相等,所以每间隔c个数据,取一次数据值,即为一个有效的边界值。对于排序后的序列,有。所得到的二维值对,即是等深度直方图。2.2算法步骤用户输入数据分桶的数目K,然后按如下步骤计算:(1)对样本数据进行排序(2)计算宽度w和c(2)对数据进行扫描和计算等宽度直方图的数目值和等深度直方图的边界2.3程序流程图图1等宽度直方图流程图在图1中,数据的分桶数目是用户输入的数据,预先由用户设定。样本数据存放在文本文件eggs.txt中,由程序运行时读入。在实验中,通过对样本数据的考察,计算桶宽度w的方法是。统计结果存放在数组中,返回统计结果。获取分桶数目k读入文件数据数据顺序排序计算桶的深度p,每个桶的数目c开始结束ie图2等深度直方图流程图在图2中,数据的分桶数目是用户输入的数据,预先由用户设定。样本数据存放在文本文件eggs.txt中,由程序运行时读入。每个桶的数据量c的计算公式,N表示原始数据的数据个数。边界计算结果存放在数组e中,返回边界数组,计算过程结束。3实验结果分析图3等宽度直方图(K=10)统计结果图4等宽度直方图(K=20)统计结果图5等深度直方图(K=10)统计结果图6等深度直方图(K=20)统计结果上面的图分别表示K=10和K=20的情况下eggs.txt中数据的等宽度和等深度直方图的统计结果。直方图的使用是为了离散化数据。在实验中,使用每个桶的中值来代表该桶中数据的离散结果。在K=10的情况下:使用等宽度直方图,样本数据离散值为{550,1650,2750,3850,4950,6050,7150,8250,9350,10450};使用等深度直方图,样本数据的离散值为{3,43,182,403,643,981,1378,1803,2365,6770}。在K=20的情况下,使用等宽度直方图,样本数据离散值为{275,825,1375,1650,1925,2475,3025,3575,4125,4675,5225,5775,6325,6875,7425,7975,8525,9075,9625,10175,10725};使用等深度直方图,样本数据的离散值为{0,2,17,50,108,199,308,412,539,683,842,1051,1221,1368,1552,1776,2035,2338,2742,6915}。实验表明:对于采用不同的直方图和不同的桶数目K,得到不同的离散化结果。4实验结论对于上述的四种离散化结果,如何来判定哪种离散化数据的效果更好呢?一般的,离散后的数据越接近样本原始数据,则效果越好。数据离散化后,与原始数据肯定存在差异一般用误差度量这种差异大小。在这里,定义平均相对误差和最大相对误差来表示离散数据逼近原始样本数据的程度,作为离散化的评判标准。平均相对误差E定义如下:,其中,和分别表示第i个值的离散值和真实值,N表示数据总量。最大相对误差M定义如下:,其中,,,N的定义和平均相对误差中的相同。对于K=10,根据等宽...