西安建筑科技大学_大学物理作业答案VIP免费

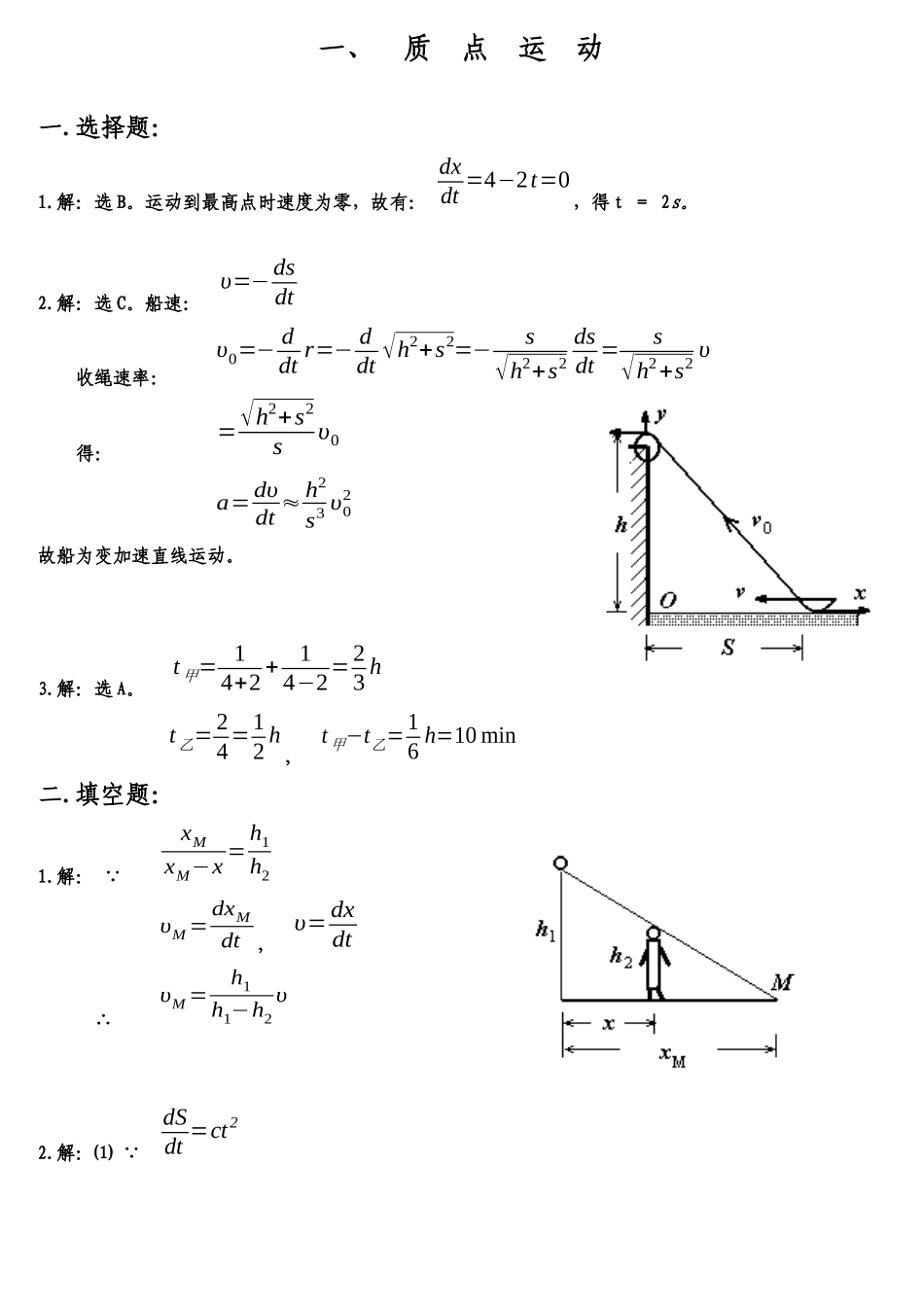
一、质点运动一.选择题：1.解：选B。运动到最高点时速度为零，故有：dxdt=4−2t=0，得t＝2s。2.解：选C。船速：υ=−dsdt收绳速率：υ0=−ddtr=−ddt√h2+s2=−s√h2+s2dsdt=s√h2+s2υ得：=√h2+s2sυ0a=dυdt≈h2s3υ02故船为变加速直线运动。3.解：选A。t甲=14+2+14−2=23ht乙=24=12h，t甲−t乙=16h=10min二.填空题：1.解： xMxM−x=h1h2υM=dxMdt，υ=dxdt∴υM=h1h1−h2υ2.解：⑴ dSdt=ct2dS=ct2dt两边积分有：∫0SdS=∫0tct2dt∴S=13ct3⑵at=dυdt=2ct⑶an=υ2R=c2t4R3.解：总加速度与半径夹45°角时，切向加速度大小等于向心加速度大小，故有：at=at2t2R，得出：t＝1s4.解：x(t)作初速度为零的加速直线运动dυxdt=Fm=t0.25=4tdυx=4tdt，积分得：υx=2t2υx=dxdt=2t2，得：dx=2t2⋅dt双方积分有：∫dx=∫2t2⋅dt，得：x=23t3y(t)作初速度为2ms-1的匀速直线运动y=υyt=2t∴r=xi+yj=23t3i+2tj(m)三.计算题：1.解：at=a+ct t=τ时at=2a∴c=aτ即at=a+atτt=nτ后，at=a+na=a(1+n)由at=dυdt，有：dυ=atdt∫0vdυ=∫0t[a+atτ]dt，得：υ=at+at22τ由υ=dsdt，ds=υdt∫0sds=∫0t[at+at22τ]dt，得：s=16at2(3+tτ)t=nτ后：s=16an2τ2(3+n)2.解：如图以⃗υ表示质点对地的速度则υx=υx'+u=√2ghcosα+uυy=υy'=√2ghsinα当y=h时，υ的大小为υ=√υx2+υy2=√u2+2gh+2u√2ghcosαυ的方向与x轴的夹角γγ=arctgυyυx=arctg√2ghsinα√2ghcosα+u四.证明题： dυdt=dυdx⋅dxdt=dυdx⋅υdυdt=−kυ2∴dυdxυ=−kυ2，得：dυυ=−kdx双方积分∫v0vdυυ=−∫0xkdx，得：υ=υ0e−kx五.问答题OA区间；AB区间υ=0a=0；BC区间a>0；CD区间a=0。二、质点动力学一.选择题：1.解：选（C）。当A紧靠在圆筒内壁而不下落时，A受到的摩擦力fr与重力平衡，又因为fr与筒壁提供给A的向心力N的反作用力的大小成正比，如图所示，故：fr=mgfr=μmRω2∴ω=√gμR2.解：选（A）。如图所示：Ncosθ=mrω2Nsinθ=mgr=Rcosθsinθ=R−hR∴ω＝12.78rad·s-1≈13rad·s-13.解：选（B）。质点m越过A角前、后的速度如图所示。由题知：θ=π3由动量定理知：I=Δ(m⃗υ)所以：I=m2υsin60°=√3mυ4.解：选（B）。初始位置矢量r=0，末位置矢量r'=2Rj则：A=F⋅dr=∫00F0xdx+∫02RF0ydy=12F0y2|2R0=2F0R25.解：选（A）。设质点m在B点的速率为υ，则由动能定理知：A摩+A重=12mυ2其中A重=mgR当质点运动到B点时下式满足：N−mg=mυ2R∴A摩=12R(N−3mg)二.填空题1.选沿着m1、m2的运动方向为X轴正向，则由受力图知：m1a1=Tm2a2=m2g−T'因为绳不伸长：T'=2Ta1=2a2∴a1=2m2g4m1+m22.(1).当弹簧长度为原长时，系统的重力势能为mgx0。又因为在O点重物平衡，即：kx0=mg，所以系统在O'点的重力势能又可表为：kx02。(2).系统的弹性势能为：−12kx02。(3).系统的总势能为kx02−12kx02=12kx02。3.坐标系和受力分析如图所示，设摩擦力为f，物体沿斜面向上方运动的距离为L，则：A=−fL=−fhsinθf=μNN+Fsinα=mgcosθ∴A=−μmgh⋅ctgθ+μFhsinαsinθ4.选弹簧压缩最大距离即O点为重力势能的零点，弹簧的自然长O'为弹性势能的零点。视物体和弹簧为物体系初态体系总能量为：mgh+mgx末态体系总能量为：12kx2体系由初态到末态的全过程中只有保守力作功.故机械能守恒。所以mgh+mgx=12kx2∴x=mgk+√(mgk)2+2mgkh三.计算题：1.设木块与弹簧接触时的动能为12mυ2。当弹簧压缩了x=0.4m时，木块的动能为零。根据动能原理：frx+12kx2=12mυ2fr=μkmg∴υ=√2μkgx+kmx2=5.83m⋅s−13.设炮车自斜面顶端滑至L处时，其速率为υ0。由机械能守恒定律知：MgLsinα=12Mυ02以炮车、炮弹为物体系，在L处发射炮弹的过程中，系统沿斜面方向的外力可以忽略，则系统沿斜面方向动量守恒。故Mυ0=mυcosα∴υ=Mmcosα√2gLsinα第三章刚体的定轴转动一.选择题：1.解：选（C）。 ⃗υ的方向不断改变，而大小不变.∴P=m⃗υ不断改变质点所受外力通过圆心，所以产生的力矩为零则角动量守恒。2.解：选（C）。根据开普勒定律得出。3.解：选（B）。解：已知：r=3i+4j+5k单位为10−2mω=60rev⋅min−1=2πs−1方向沿Z轴由⃗υ=ω×r...