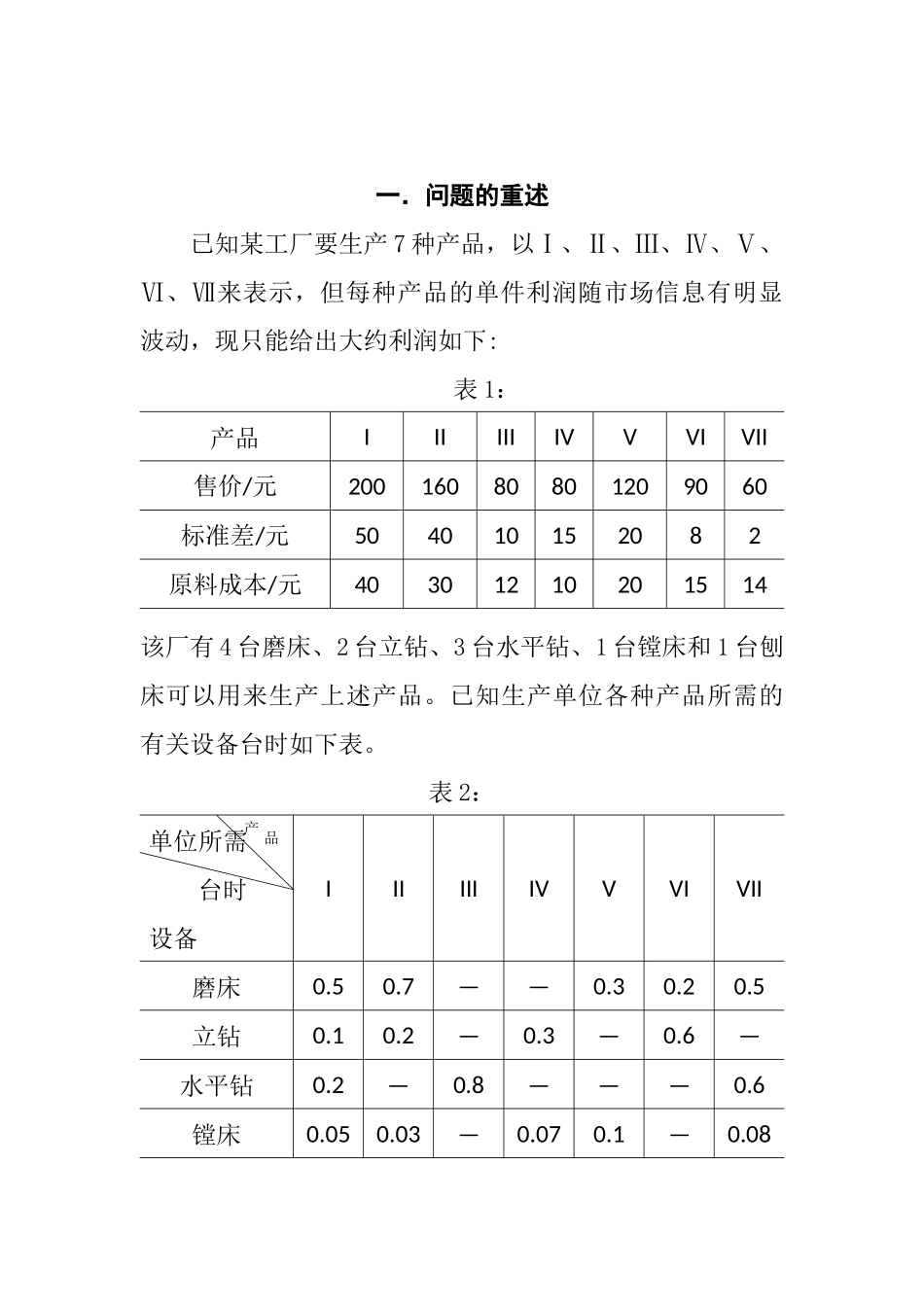
题目生产计划安排摘要本文就企业机械设备优化配置和生产安排的问题,综合考虑利润最大化及实际约束条件等因素,在合理假设的基础上,提供了以利润最大化为目标的企业生产方案的模型通过对模型的求解,得到最优的生产方案,从而有效地指导企业进行生产,以实现最大的收益。在问题一中,我们根据“利润=售价×产品销售数量-生产成本-库存费用”和“生产成本=原料成本+用电成本”为原理建立目标函数,并考虑到不同时段的生产成本生产设备、产品的最大需求量以及供电功率等方面的限制以此为依据限定约束条件,以此建立线性规划模型Ⅰ。并用LINGO软件,得到最优的的生产安排计划,以实现利润的最大化,得到最大利润为1457557元。当原材料价格上涨10%时,模型Ⅰ同样适用,将模型Ⅰ中的qj以(1+rise)×qj代替,根据模型Ⅰ计算可得到此时的最大利润为1422862元,发现生产计划不用改变。对原料价格进行灵敏度分析后发现,当原料价格上涨或下降在12.43%以内时,生产计划不用改变。问题二是在维修计划未限制的情况下,要求合理安排生产及维修计划,实现利润的最大化。其中,我们发现六个月中每种设备可用的总台数不变。为此,我们在模型Ⅰ的基础上,目标函数不变,改变关于每种设配可用台数的约束条件,建立新的线性规划模型,即模型Ⅱ,求解出合理的维修和生产计划,得到此时的最大利润为1640789元。进行灵敏度分析后发现,当原料价格上涨或下降在7.6%以内时,生产计划不用改变。问题三中由于供电紧张,5-6月仅供应50Kw的电力,所以需要对生产计划做出调整。为此,我们在模型Ⅰ的基础上,目标函数不变,在约束条件中,对5、6月份的用电功率限制做出修改,从而建立线性规划模型Ⅲ,以制定出新的生产计划,得到此时的最大利润为1456992元。关键词:整数线性规划LINGO最优解生产方案灵敏度分析产品一.问题的重述已知某工厂要生产7种产品,以Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ来表示,但每种产品的单件利润随市场信息有明显波动,现只能给出大约利润如下:表1:产品IIIIIIIVVVIVII售价/元20016080801209060标准差/元504010152082原料成本/元40301210201514该厂有4台磨床、2台立钻、3台水平钻、1台镗床和1台刨床可以用来生产上述产品。已知生产单位各种产品所需的有关设备台时如下表。表2:单位所需台时设备IIIIIIIVVVIVII磨床0.50.7——0.30.20.5立钻0.10.2—0.3—0.6—水平钻0.2—0.8———0.6镗床0.050.03—0.070.1—0.08刨床——0.01—0.05—0.05从1月到6月,维修计划如下:1月—1台磨床,2月—2台水平钻,3月—1台镗床,4月—1台立钻,5月—1台磨床和1台立钻,6月—1台刨床和1台水平钻,被维修的设备当月不能安排生产。若每台设备的功率如下:磨床,5kw;立钻8kw;水平钻6Kw;镗床8kw;刨床12kw供电功率为70Kw;电价:0-8时0.8元/kwh;8-24时1.2元/kwh。又知从1—6月市场对上述7中产品最大需求量如下表所示:表3:IIIIIIIVVVIVII1月100015003003008002001002月80060020004003001503月400600005004001004月40050040050020001005月100200500100100030006月800400300300150050080每种产品当月销售不了的每件每月存储费为5元,但规定任何时候每种产品的存储量均不能超过100件。1月初无库存,要求6月末各种产品各储存50件。若该工厂每月工作30天,每天三班(0-8时;8-16时;16-24时),每班8小时,要求:(1)该厂如何安排生产,使企业利润最大;若原材料价格上涨10%,如何安排生产。(2)若对设备维修只规定每台设备在1—6月份内均需安排1个月用于维修(其中4台磨床只需安排2台在上半年维修),时间可灵活安排。重新为该厂确定一个最优的设备维修计划。(3)由于供电紧张;5-6月仅供应50Kw的电力,如何调整计划。二.问题的分析2.1问题一的分析问题一要求合理安排生产实现利润的最大化。问题中提供了生产设备方面的限制及产品的最大需求量,要求安排各月的生产计划,因此可以根据“利润=售价×产品销售数量-生产成本-库存费用”和“生产成本=原料成本+用电成本”为原理建立目标函数,其中,“原料成本=单件原料成本×产品生产量”,而用电成本可分为0-8时的用电成本和8-24时的用电成本,即“用电成本...