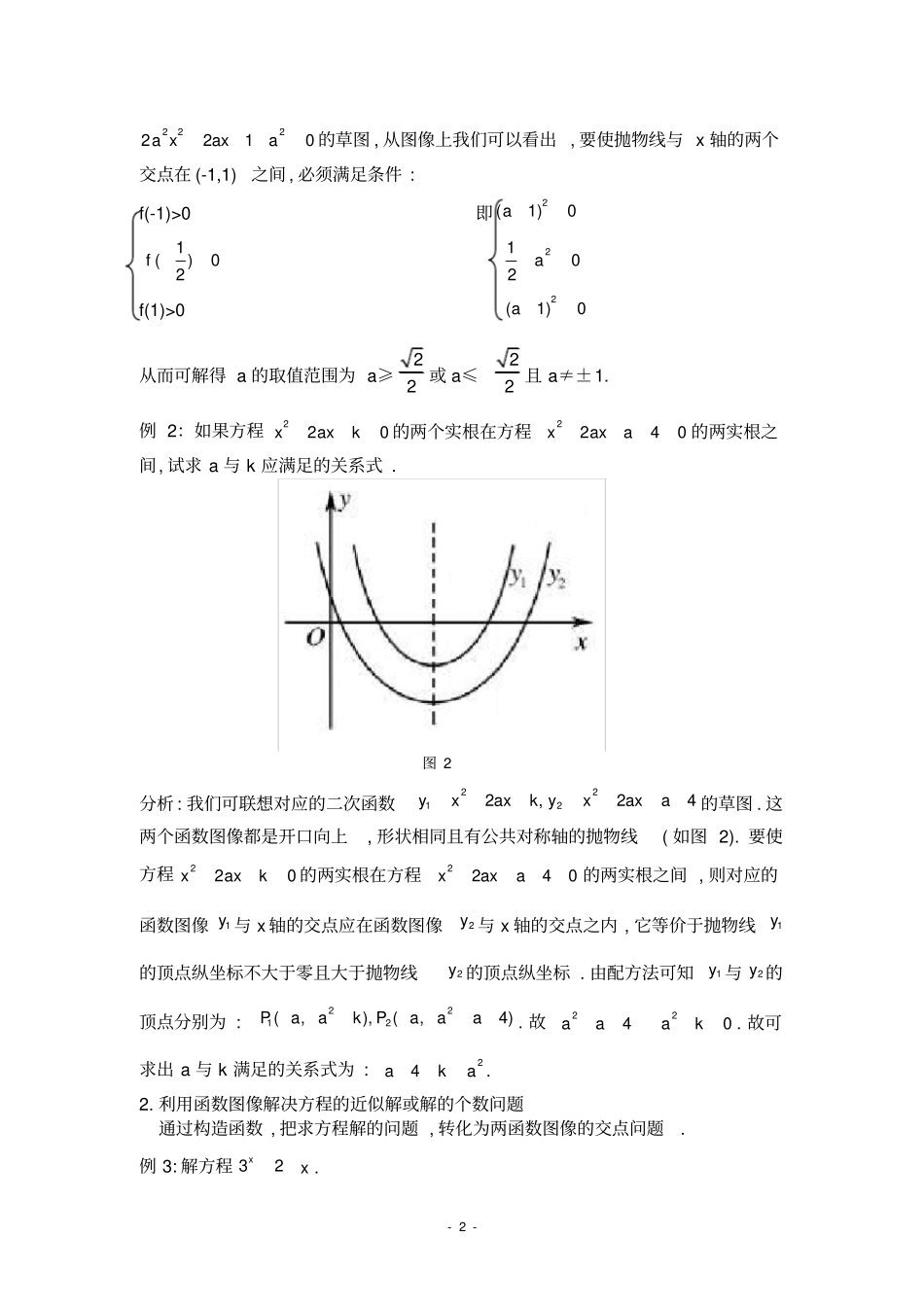
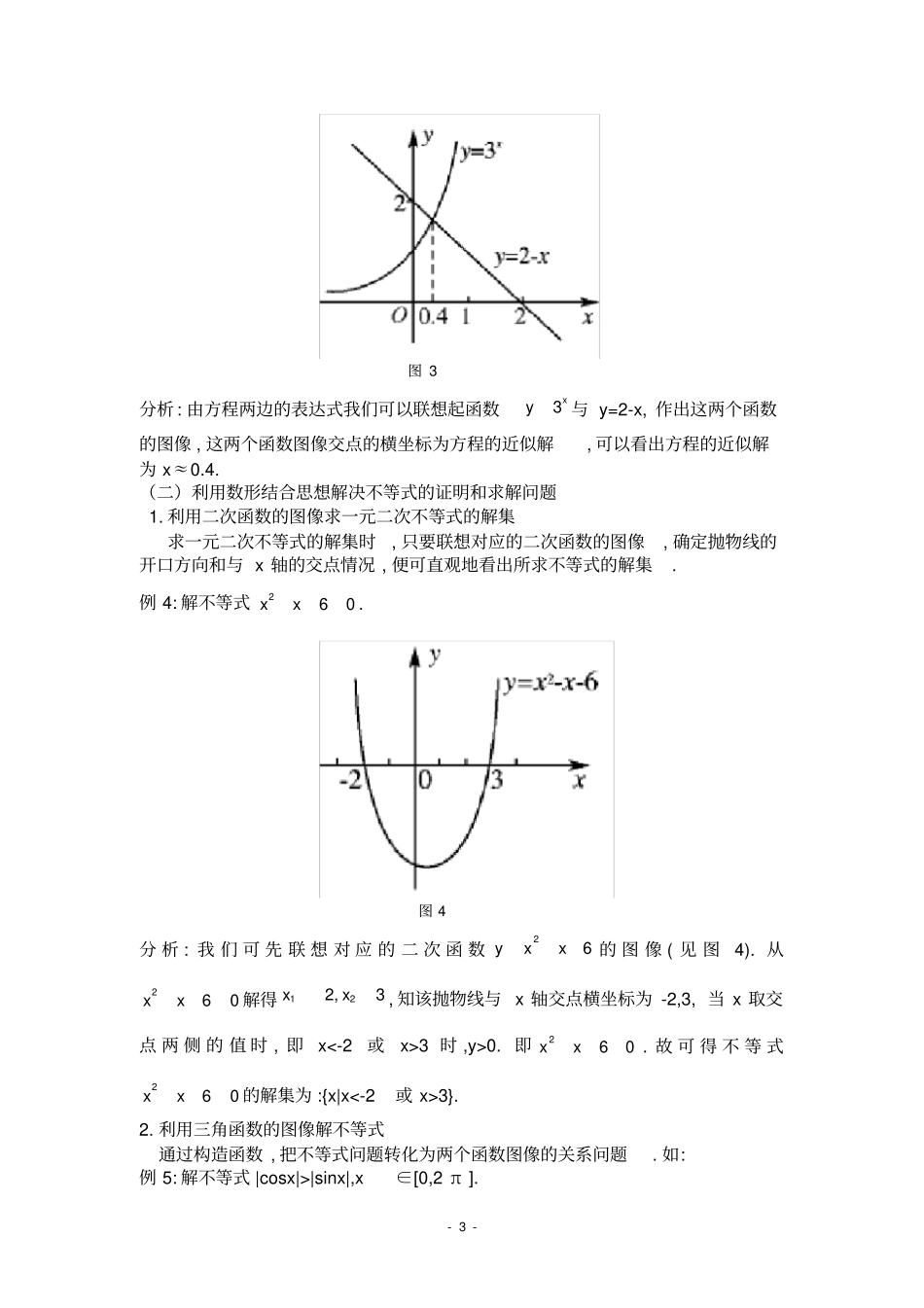
-1-数形结合在初等数学解题中的应用学生姓名:马文静指导教师:郝建华引言:数形结合是中学数学中重要的思想方法之一,是数学的本质特征。华罗庚先生曾指出:数缺形时少直观,形少数时难入微;数形结合百般好,隔裂分家万事非。就代数本身而言,缺乏直观性,就几何本身而言,缺乏严密性。只有将二者有机地结合起来,互相取长补短,才能突破思维的限制,加快数学的发展。法国数学家拉格朗日所指出的“只要代数同几何分道扬镶,它们的进展就缓慢,它们的应用就狭窄,但是当两门科学结合成伴侣时,它们就相互吸取新鲜的活力,从那以后,就以快速的步伐走向完善”。在解决数学问题时,将抽象的数学语言同直观的图形相结合,实现抽象的概念与具体形象的联系和转化,使数与形的信息相互渗透,可以开拓我们的解题思路,使许多数学问题简单化。一、利用数形结合思想解代数问题借助图形直观地研究数学问题,不仅可以加深对数量关系的理解,而且还可以简化运算过程。(一)利用数形结合思想解决方程问题1.利用二次函数的图像解决一元二次方程根的分布情况问题利用函数y=f(x)的图象直观解决问题。例1:a为何值时,方程2222210axaxa的两根在(-1,1)之内?图1分析:显然2a≠0,我们可从已知方程联想到相应的二次函数-2-2222210axaxa的草图,从图像上我们可以看出,要使抛物线与x轴的两个交点在(-1,1)之间,必须满足条件:f(-1)>0即2(1)0a1()02f2102af(1)>02(1)0a从而可解得a的取值范围为a≥22或a≤22且a≠±1.例2:如果方程220xaxk的两个实根在方程2240xaxa的两实根之间,试求a与k应满足的关系式.图2分析:我们可联想对应的二次函数22122,24yxaxkyxaxa的草图.这两个函数图像都是开口向上,形状相同且有公共对称轴的抛物线(如图2).要使方程220xaxk的两实根在方程2240xaxa的两实根之间,则对应的函数图像1y与x轴的交点应在函数图像2y与x轴的交点之内,它等价于抛物线1y的顶点纵坐标不大于零且大于抛物线2y的顶点纵坐标.由配方法可知1y与2y的顶点分别为:2212(,),(,4)PaakPaaa.故2240aaak.故可求出a与k满足的关系式为:24aka.2.利用函数图像解决方程的近似解或解的个数问题通过构造函数,把求方程解的问题,转化为两函数图像的交点问题.例3:解方程32xx.-3-图3分析:由方程两边的表达式我们可以联想起函数3xy与y=2-x,作出这两个函数的图像,这两个函数图像交点的横坐标为方程的近似解,可以看出方程的近似解为x≈0.4.(二)利用数形结合思想解决不等式的证明和求解问题1.利用二次函数的图像求一元二次不等式的解集求一元二次不等式的解集时,只要联想对应的二次函数的图像,确定抛物线的开口方向和与x轴的交点情况,便可直观地看出所求不等式的解集.例4:解不等式260xx.图4分析:我们可先联想对应的二次函数26yxx的图像(见图4).从260xx解得122,3xx,知该抛物线与x轴交点横坐标为-2,3,当x取交点两侧的值时,即x<-2或x>3时,y>0.即260xx.故可得不等式260xx的解集为:{x|x<-2或x>3}.2.利用三角函数的图像解不等式通过构造函数,把不等式问题转化为两个函数图像的关系问题.如:例5:解不等式|cosx|>|sinx|,x∈[0,2π].-4-分析:不等式两边的表达式我们可以看成两个函数1y=|cosx|,2y=|sinx|.在[0,2π]上作出它们的图像(图5),得到四个不同的交点,横坐标分别为:4,34,54,74,而当x在区间[0,4),(34,54),(74,2π]内时,1y=|cosx|的图像都在2y=|sinx|的图像上方.所以可得到原不等式的解集为:{0≤x<4或3412.图6分析:因为正弦线在单位圆中是用方向平行于y轴的有向线段来表示.我们先在y轴上取一点P,使OP=12恰好表示角x的正弦线sinx=12,过点P作x轴的平图5-5-行线交单位圆于点1P,2P(如图6),在[3,22]内,12,OPOP分别对应于角7,66,(这时所对应的正弦值恰好为12).而要求sinx>12的解集,只需将弦12PP向上平移,使12,OPOP重合(也即点P向上平移至与单位圆交点处).这样12,OPOP所扫过的范围即为所求的角.原不等...