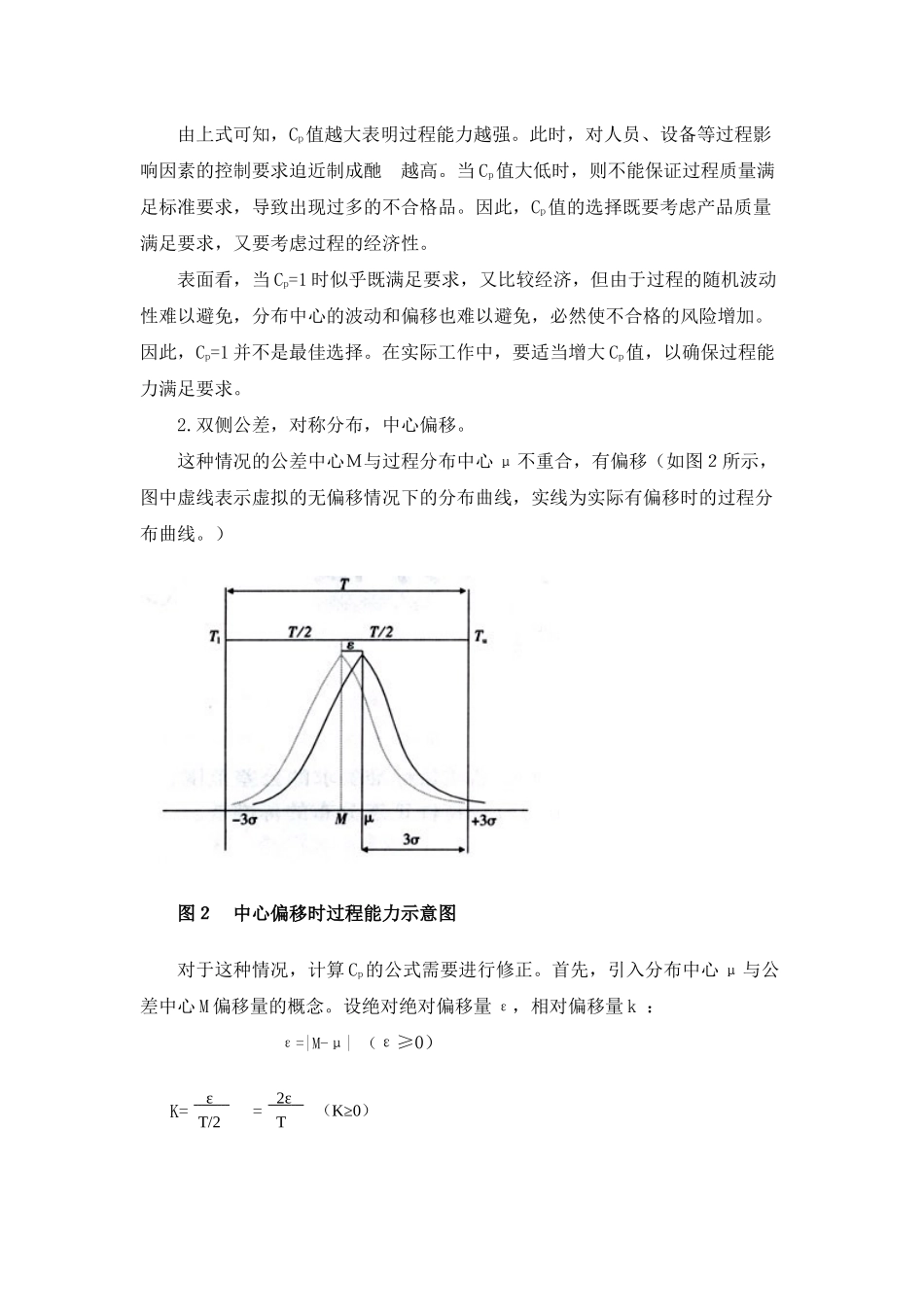
过程能力的确认方法ISO9001:2000标准的7.5.2条款规定:“当生产和服务提供过程的输出不能由后续的影视或测量加以验证时,组织应对任何这样的过程实施确认。这包括仅在产品使用或服务已交付之后问题才显现的过程。”实际上,这里所说的需要实施确认的过程就是特殊过程。由于许多企业对这个条款的规定感到难以实施,笔者谈一些对过程能力实施确认的方法。一、过程确认与过程能力7.5.2条款要求对特殊过程实施确认,并明确提出:“确认应证实这些过程实现所策划的结果的能力。”所谓过程能力,就是在受控条件下,保证过程能够生产合格产品的能力。任何过程的运行都会受到许多因素的影响,这些影响因素大致可分为两大类:一是系统性影响因素,二是随机性影响因素。系统性影响因素能使过程产生系统性波动,这类波动的数值较大或具有一定的规律性,这是我们所不期望的,应该力加避免。所谓使过程在受控条件下运行,就是要对系统性因素实施有效控制,不允许过程在系统性因素的影响下运行。随机性影响因素能使过程产生随机性波动,这种波动的数值比较小,从微观上说波动没有规律,是很多微弱影响因素综合作用的结果。这类波动无法(或不值得)从技术的角度加以克服,只能利用统计学的规律对其进行研究。大多数随机波动服从统计学的正态分布规律。综上所述,当过程受控并消除了系统性波动,在随机状态下运行,就可以用随机状态的正态分布规律讨论过程的能力。在正态分布时,其特征值一般用正态分布的标准差δ表示,过程能力通常用6δ表示,其中“δ”常被视为过程能力的度量单位。过程能力指数是表示过程能力满足产品质量标准要求(包括产品规格要求和公差要求)的程度。在无偏移的情况下通常记作:Cp=T6δ式中:Cp为过程能力指数;T为产品质量标准要求的公差范围;δ为过程特性正态分布的标准差。二、正态分布下过程能力指数的计算方法根据过程质量的客观分布规律与质量标准要求相对关系的不同,正态分布下的过程能力指数计算方法,大致可分为下列四种情况。1.双侧公差,对称分布,中心重合。这是产品质量标准要求的公差双侧对称分布,其公差中心M与过程质量特性分布中心μ相重合,无偏移(如图1所示)。其过程能力指数Cp为:Cp=Tμ-T1=T3δ-(-3δ)6δ式中:Tμ为产品质量标准要求的规格上限值;T1为产品质量标准要求规格下限值;图1中心无偏移过程能力示意图由上式可知,Cp值越大表明过程能力越强。此时,对人员、设备等过程影响因素的控制要求迫近制成酏越高。当Cp值大低时,则不能保证过程质量满足标准要求,导致出现过多的不合格品。因此,Cp值的选择既要考虑产品质量满足要求,又要考虑过程的经济性。表面看,当Cp=1时似乎既满足要求,又比较经济,但由于过程的随机波动性难以避免,分布中心的波动和偏移也难以避免,必然使不合格的风险增加。因此,Cp=1并不是最佳选择。在实际工作中,要适当增大Cp值,以确保过程能力满足要求。2.双侧公差,对称分布,中心偏移。这种情况的公差中心M与过程分布中心μ不重合,有偏移(如图2所示,图中虚线表示虚拟的无偏移情况下的分布曲线,实线为实际有偏移时的过程分布曲线。)图2中心偏移时过程能力示意图对于这种情况,计算Cp的公式需要进行修正。首先,引入分布中心μ与公差中心M偏移量的概念。设绝对绝对偏移量ε,相对偏移量k:ε=|M-μ|(ε≥0)K=ε=2ε(K≥0)T/2T因为µ与M之间的偏移,引起了“吃容差”的现象。当过程分布中心向右偏移时(见图2),会吃上偏差(右半边的偏差);当分布中心向左偏移时,会吃下偏差(左半边的偏差)。这时,过程出现不合格吕的危险首先出现在被吃掉容差的一边。因此,计算过程能力指数时,可以只考虑分布中心偏移后引起喷气发动机容不得差的半边。按照图2的情况,CP的计算公式如下:Cp=T-ε=2(1-2ε)T=(1-k)T¯¯¯¯¯¯¯¯T6δ6δ3δ当µ=M,即分布中心与公关中心相重合时,ε=0、κ=0,导致CP=,这是无偏移的情况。当µ与M发生相对偏移,且µ偏移至公差的上限T1或偏至下限,即µ=Tu或µ=T1时,ε=T/2、κ=1、CP=0(当偏移使µ越过Tu或T1时,...