解直角三角形的实际应用导学案VIP免费

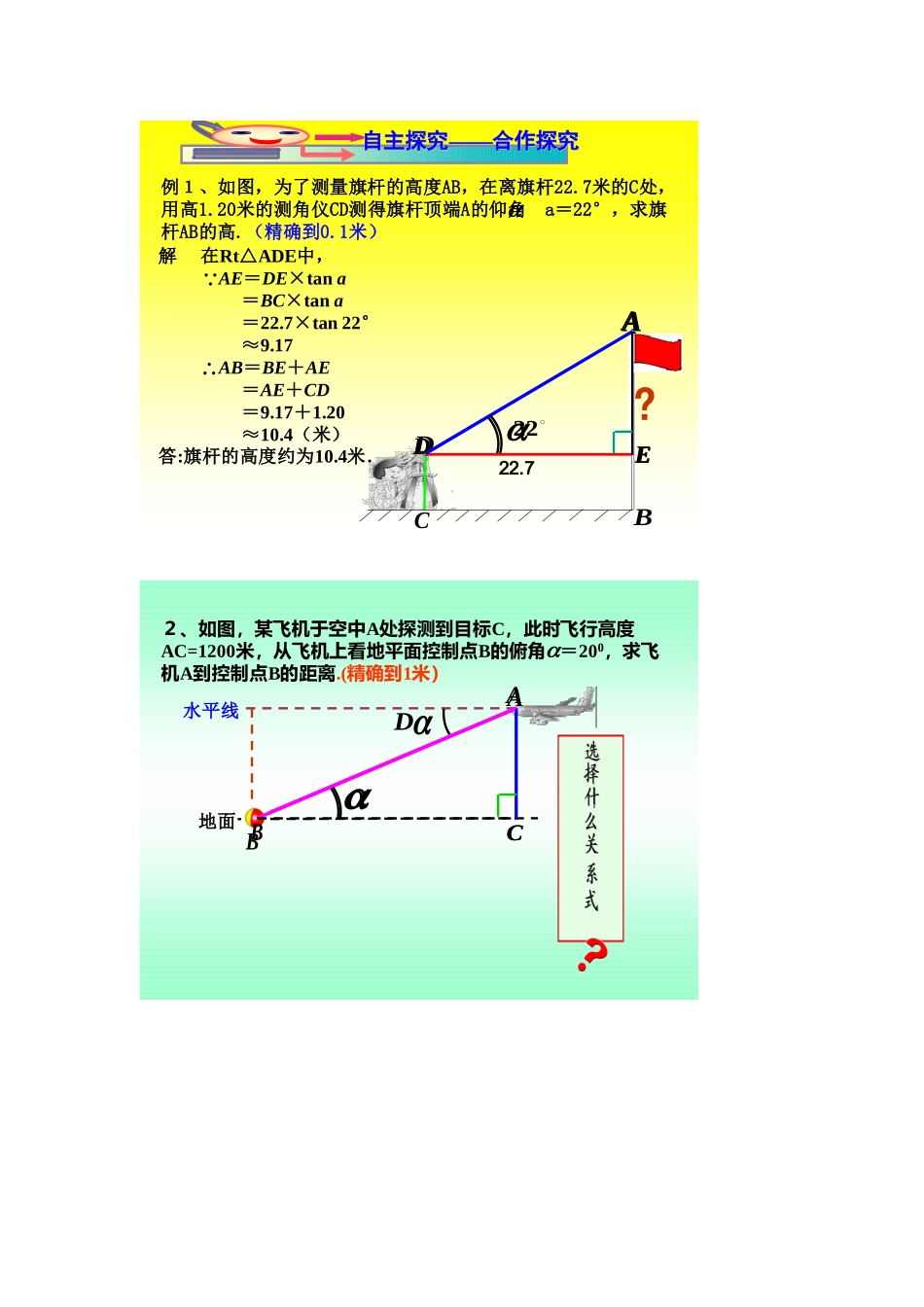
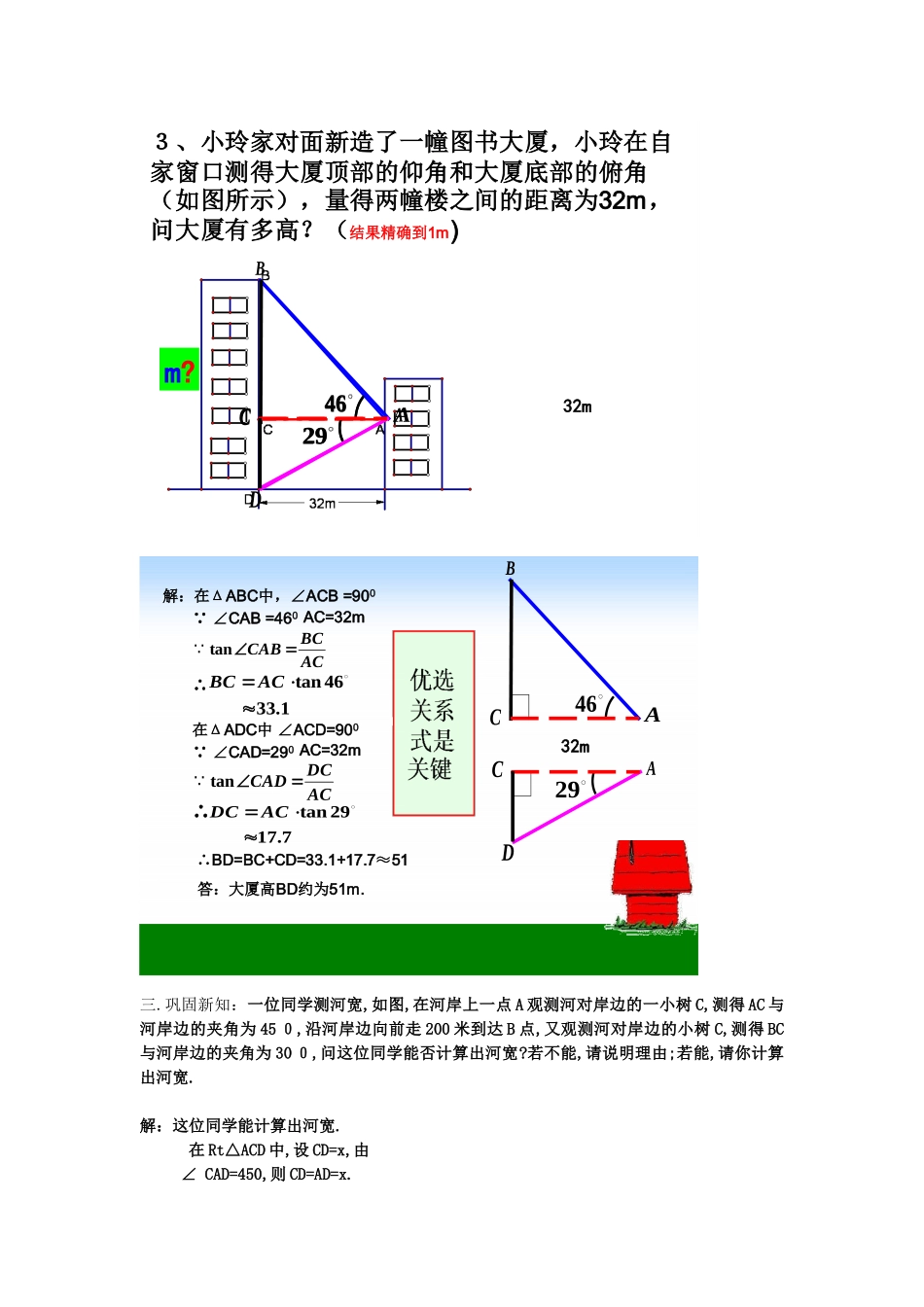
解直角三角形的实际应用---------仰角、俯角问题导学案教学目标：1.掌握仰角、俯角的定义2.会运用解直角三角形的有关知识解决实际应用问题。情感目标：了解数学知识来源于生活，并应用于生活。重点、难点：将实际问题中的数量关系归结为直角三角形中的元素之间的关系。教学过程：一：自主学习温故而知新：直角三角形三边的关系，锐角之间的关系，边与角之间的关系（以∠A为例）接着学生自主学习：请同学们自学教材P95页的内容，独立解决以下问题：1.什么叫仰角？2.什么叫俯角？3.本课导语的图中有仰角和俯角吗？若有，请指出其中的仰角和俯角。二．合作探究：ABED解在Rt△ADE中，AE＝DE×tana＝BC×tana＝22.7×tan22°≈9.17AB＝BE＋AE＝AE＋CD＝9.17＋1.20≈10.4（米）答:旗杆的高度约为10.4米．∵∴C自主探究自主探究————合作探究合作探究?22.722EAD例１、如图，为了测量旗杆的高度AB，在离旗杆22.7米的C处，用高1.20米的测角仪CD测得旗杆顶端A的仰角a＝22°，求旗杆AB的高.（精确到0.1米）A水平线地面DCBACB２、如图，某飞机于空中A处探测到目标C，此时飞行高度AC=1200米，从飞机上看地平面控制点B的俯角＝200，求飞机A到控制点B的距离.(精确到1米）３、小玲家对面新造了一幢图书大厦，小玲在自家窗口测得大厦顶部的仰角和大厦底部的俯角（如图所示），量得两幢楼之间的距离为32m，问大厦有多高？（结果精确到1m)4629m?46ABCC29DA32m32m46ABCC29DAAC=32m解：在ΔABC中，∠ACB=900∵∠CAB=460∴在ΔADC中∠ACD=900∵∠CAD=290ACDCCADtan∴BD=BC+CD=33.1+17.7≈51答：大厦高BD约为51m.AC=32mACBCCABtan7.1729tanACDC1.3346tanACBC∴三.巩固新知：一位同学测河宽,如图,在河岸上一点A观测河对岸边的一小树C,测得AC与河岸边的夹角为45０,沿河岸边向前走200米到达B点,又观测河对岸边的小树C,测得BC与河岸边的夹角为30０,问这位同学能否计算出河宽?若不能,请说明理由;若能,请你计算出河宽.解：这位同学能计算出河宽.在Rt△ACD中,设CD=x,由∠CAD=450,则CD=AD=x.在Rt△BCD中,AB=200,则BD=200+X,由∠CBD=300,则tan30°=CD／BD解得x=100√3+100所以河宽为100√3+100四．大展身手：1、一架飞机以300角俯冲400米,则飞机的高度变化情况是()A.升高400米B.下降400米C.下降200米D.下降200√3米2、在山顶上D处有一铁塔，在塔顶B处测得地面上一点A的俯角α=60o，在塔底D测得点A的俯角β=45o，已知塔高BD=30米，则山高CD=__________米.五．小结与思考谈谈你的收获六．作业