黑龙江省绥化市第九中学九年级数学上册《勾股定理》导学案 新人教版VIP免费

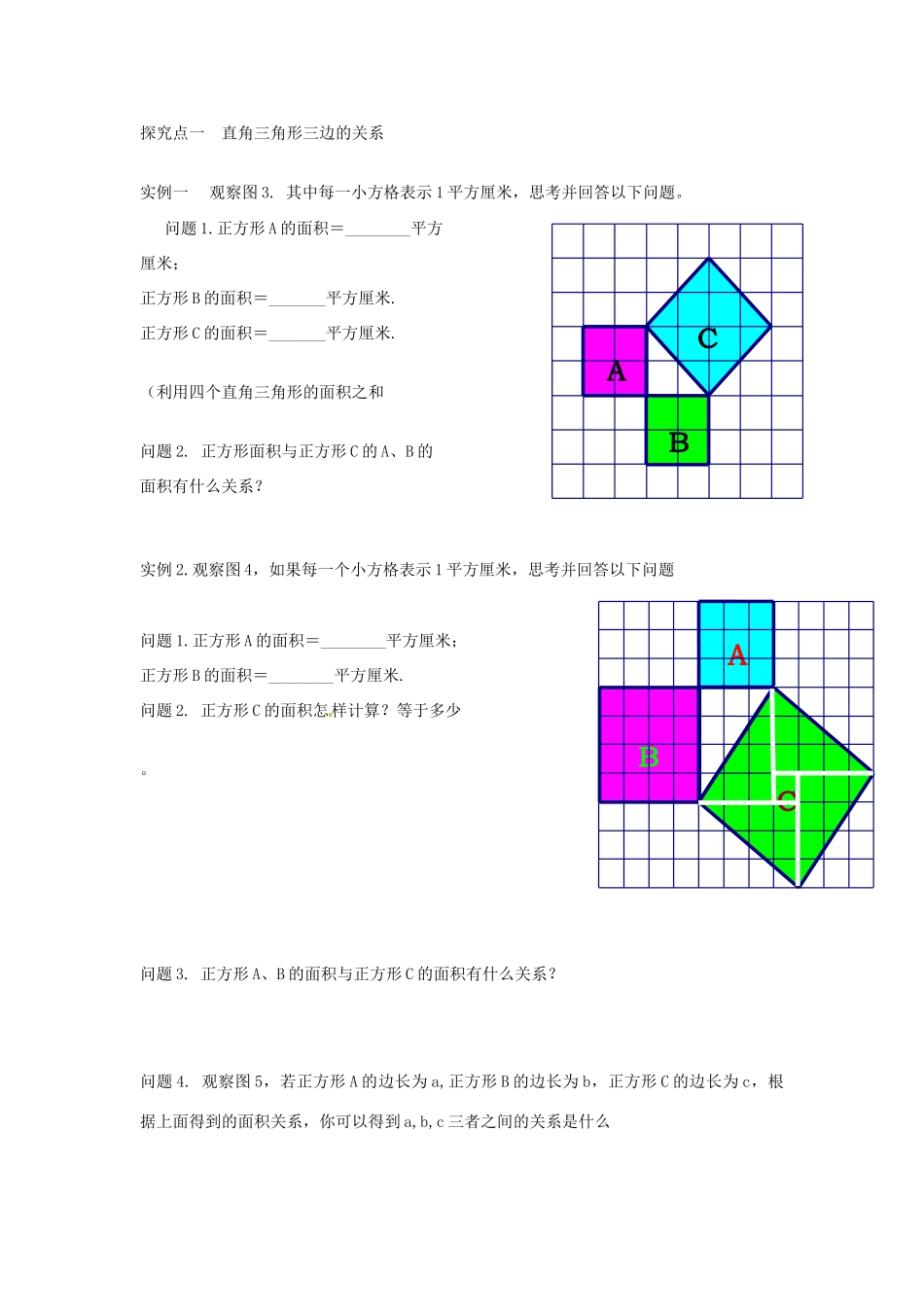
第18章勾股定理导学案(一)《学习目标》1.掌握勾股定理的内容，会用面积法证明勾股定理。提高发现问题总结规律的能力；2.通过独立思考、小组合作、动手操作，探究并归纳出勾股定理的证明方法；3.以极度的热情投入学习，全力以赴享受成功学习的快乐。(二)重点：勾股定理的内容及证明(三)难点：勾股定理的证明预习案预习学法指导1、用15分钟左右的时间，阅读探究课本的基础知识。2、完成教材助读设置的问题，然后结合课本的基础知识例题，完成预习自测。3、将预习中不能解决的问题标出来，并写到后面“我的疑惑”处，以便向老师请教或小组合作探究。4、限时高质完成，可以用双色笔作修改补充。案（一）.旧知回顾1.三角形的面积公式是什么？2.三角形三个内角的关系如何？直角三角形两个锐角之间的关系如何？3.三角形三边关系如何？4.具有什么特征的三角形是直角三角形？（二）教材助读1.在图18.1-1中，上面的两个小蓝正方形的边长是多少？面积又是多少？2.在图18.1-1中，下面的大红正方形的边长是多少？面积又是多少？3.两个小蓝正方形的面积与大红正方形的面积有什么关系？由此你可以归纳出这三个正方形围成的小直角三角形的边长有什么关系？4.勾股定理适用于什么三角形？(三)预习自测1.勾股定理的具体内容是2.如图1，RT⊿ABC的主要性质是：_________________（！）两锐角之间的关系：_________________（2）若D为斜边AB的中点，则______________________（3）.若∠B＝30°则______________________（4）三边之间的关系：_________________________我的疑惑？探究案如图2所示，直角三角形ABC中，直角三角形的三条边之间有什么关系。这就是我们本节课要学习的内容。(四)学始于疑————我思考、我收获1.对于一般直角三角形，你能利用面积法验证勾股定理吗？2.你能用过股定理解决我们课本上的探究1吗？不妨试一试。(二)质疑探究质疑解疑、合作探究（一）基础知识探究本探究点考查学生的动手操作能力，老师应经主动权教给学生，让学生尽情享受自己学习带来的快乐。探究点一直角三角形三边的关系实例一观察图3.其中每一小方格表示1平方厘米，思考并回答以下问题。问题1.正方形A的面积＝________平方厘米；正方形B的面积＝_______平方厘米.正方形C的面积＝_______平方厘米.（利用四个直角三角形的面积之和问题2.正方形面积与正方形C的A、B的面积有什么关系？实例2.观察图4，如果每一个小方格表示1平方厘米，思考并回答以下问题问题1.正方形A的面积＝________平方厘米；正方形B的面积＝________平方厘米.问题2.正方形C的面积怎样计算？等于多少。问题3.正方形A、B的面积与正方形C的面积有什么关系？问题4.观察图5，若正方形A的边长为a,正方形B的边长为b，正方形C的边长为c，根据上面得到的面积关系，你可以得到a,b,c三者之间的关系是什么ABCABCC探究点二：勾股定理的证明实例1:利用四个边长是a，b，c的直角三角形，拼成下面的一个大正方形.动手做一做，探究下列问题：问题1.你能表示图6中大正方形、小正方形面积吗？问题2.你能由此得到勾股定理吗？你能给出证明吗？.（二）知识综合应用探究探究点三：勾股定理的应用（重点、难点）ABCCabcabc【例1】在Rt△ABC中，∠Ｃ=90°.(1)已知：a=6，ｂ=8，求c；(2)已知：a=40，c=41，求b；(3)已知：c=13，b=5，求a；(4)已知:a:b=3:4,c=15,求a、b思考1.勾股定理内容是什么？若已知两直角边长度是a,b,则斜边c=.思考2.若已知直角边a和斜边c的长度，另一直角边b=______.探究点二：勾股定理的实际应用【例2】一个门框的尺寸如图所示，一块长3m，宽2.2m的薄木板能否从门框内通过?为什么?例3：一架长为10m的梯子AB斜靠在墙上，若梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑2m,那么它的底端是否也滑动2m?三.的知识网络图———归纳梳理、整合内化请同学们对本节所学相关知识归纳总结后，填写下面的知识网络图：：勾股定理__a2＋b2=c2勾股定理勾股定理的变形：a2=c2-b2,b2=c2-a2四.当堂检测———有效训练、反馈矫正1.已知一个直角三角形的两边长分别为3和4，则第三边长的平方是（）A.25B.14C.7D.7或252.如图10，阴影部分是以直角三角形的一直角边的正...