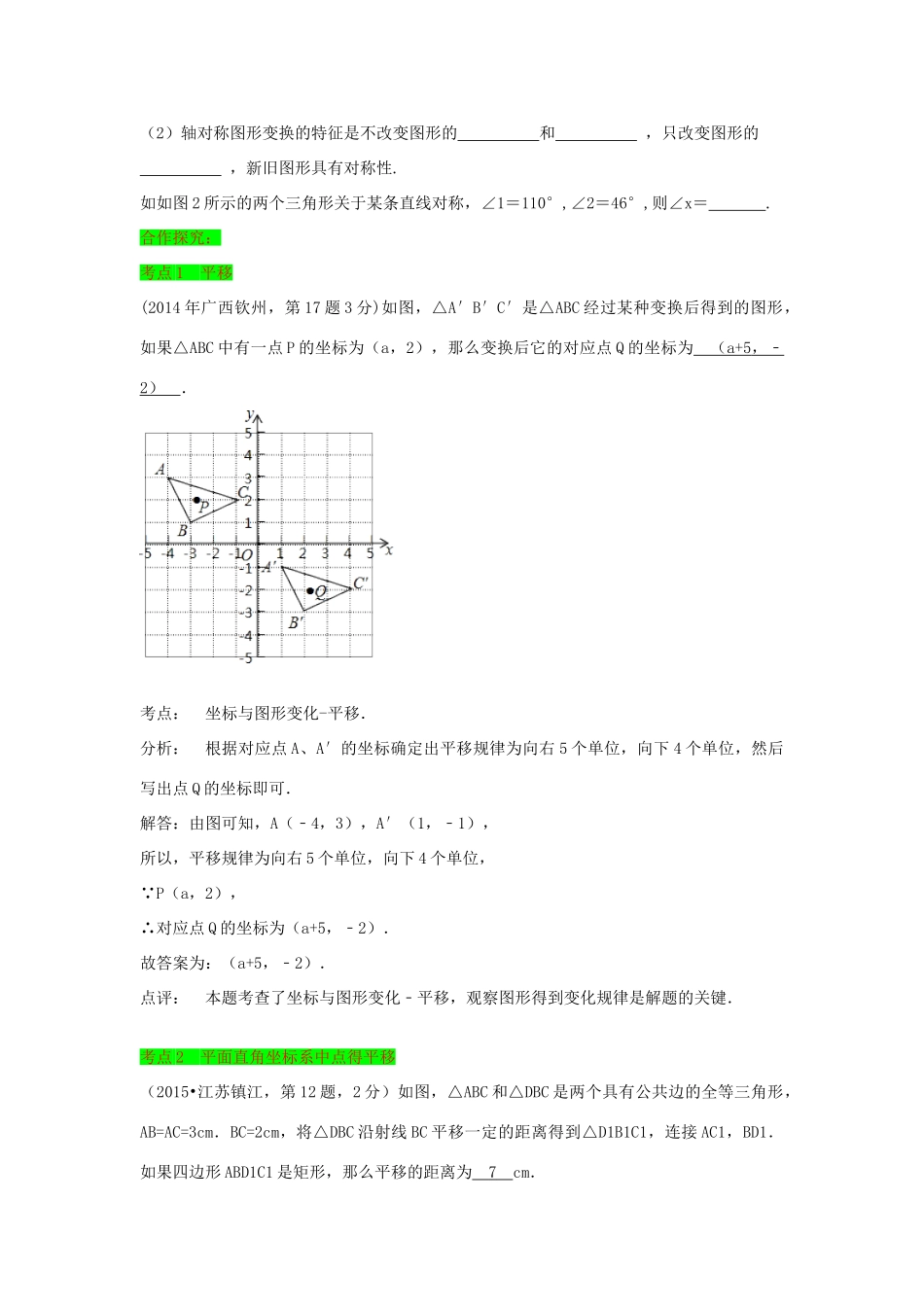
平移与轴对称学习目标:1.认识平移,理解平移的概念和平移的基本性质;2.能按要求作出简单平面图形平移后的图形,能探索图形之间的平移关系;3.理解轴对称及轴对称图形.掌握轴对称图形的性质;4.能根据要求正确地作出轴对称图形,并利用轴对称进行简单的图案的设计;5.掌握基本图形(平行四边形.矩形.菱形.正方形,圆)的轴对称性;6.了解平面坐标系中两点的对称性.并能得出对称点的坐标.复习反馈:1.图形的平移.(1.)定义:在平面内,将某个图形沿某个______移动一定的_______,这样的图形运动为平移;平移后,对应角________且对应角两边分别平行.方向相同.平移不改变图形的______.(2)性质:平移后,对应线段相等且平行,对应点所连的线段______且________,______和______只改变图形位置,平移后新旧两图形全等.(3)如图,△ABC平移到△A'B'C'|平行且相等的线段有相等的角有2.轴对称、轴对称图形(1)轴对称图形:如果一个图形沿某条直线对折,对折的两部分是的,那么就称这样的图形为轴对称图形.这条直线称为,一定为直线.(2)轴对称:把一个图形沿着某一条直线翻折过去,如果它能与另一个图形重合,那么这两个图形成,两个图形中的对应点叫.如图1,下列图案是我国几家银行的标志,其中不是轴对称图形的是()2.轴对称图形的性质(1)轴对称图形的对应线段,对应角,对应点的连线被对称轴.轴对称的两个图形,对应线段或延长线相交,交点在上.2图ABCD图1ABCA'B'C'(2)轴对称图形变换的特征是不改变图形的和,只改变图形的,新旧图形具有对称性.如如图2所示的两个三角形关于某条直线对称,∠1=110°,∠2=46°,则∠x=.合作探究:考点1平移(2014年广西钦州,第17题3分)如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为(a+5,﹣2).考点:坐标与图形变化-平移.分析:根据对应点A、A′的坐标确定出平移规律为向右5个单位,向下4个单位,然后写出点Q的坐标即可.解答:由图可知,A(﹣4,3),A′(1,﹣1),所以,平移规律为向右5个单位,向下4个单位, P(a,2),∴对应点Q的坐标为(a+5,﹣2).故答案为:(a+5,﹣2).点评:本题考查了坐标与图形变化﹣平移,观察图形得到变化规律是解题的关键.考点2平面直角坐标系中点得平移(2015•江苏镇江,第12题,2分)如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为7cm.考点:相似三角形的判定与性质;等腰三角形的性质;矩形的性质;平移的性质..分析:作AE⊥BC于E,根据等腰三角形的性质和矩形的性质求得∠BAE=∠AC1B,∠AEB=∠BAC1=90°,从而证得△ABE∽△C1BA,根据相似三角形对应边成比例求得BC1=9,即可求得平移的距离即可.解答:解:作AE⊥BC于E,∴∠AEB=∠AEC1=90°,∴∠BAE+∠ABC=90° AB=AC,BC=2,∴BE=CE=BC=1, 四边形ABD1C1是矩形,∴∠BAC1=90°,∴∠ABC+∠AC1B=90°,∴∠BAE=∠AC1B,∴△ABE∽△C1BA,∴= AB=3,BE=1,∴=,∴BC1=9,∴CC1=BC1﹣BC=9﹣2=7;即平移的距离为7.故答案为7.点评:本题考查了等腰三角形的性质,矩形的性质,三角形相似的判定和性质,作出辅助线构建相似三角形是解题的关键.考点3平面直角坐标系中的点对称.(2015•铜仁市)(第14题)已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=﹣6.考点:关于x轴、y轴对称的点的坐标分析:根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得a=2,b=﹣3,进而可得答案.解答: 点P(3,a)关于y轴的对称点为Q(b,2),∴a=2,b=﹣3,∴ab=﹣6,故答案为:﹣6.点评:此题主要考查了关于y轴对称点的坐标特点,关键是掌握点的坐标的变化规律.考点4轴对称与轴对称图形(2015,广西钦州,1,3分)下列图形中,是轴对称图形的是()A.B.C.D.考点:轴对称图形.分析:根据轴对称图形的概念对各图形分析判断即可得解.解答:解:A、该图形不是轴对称图形,故本选项错误;B、该图形是中心对称图形,故本选项错...