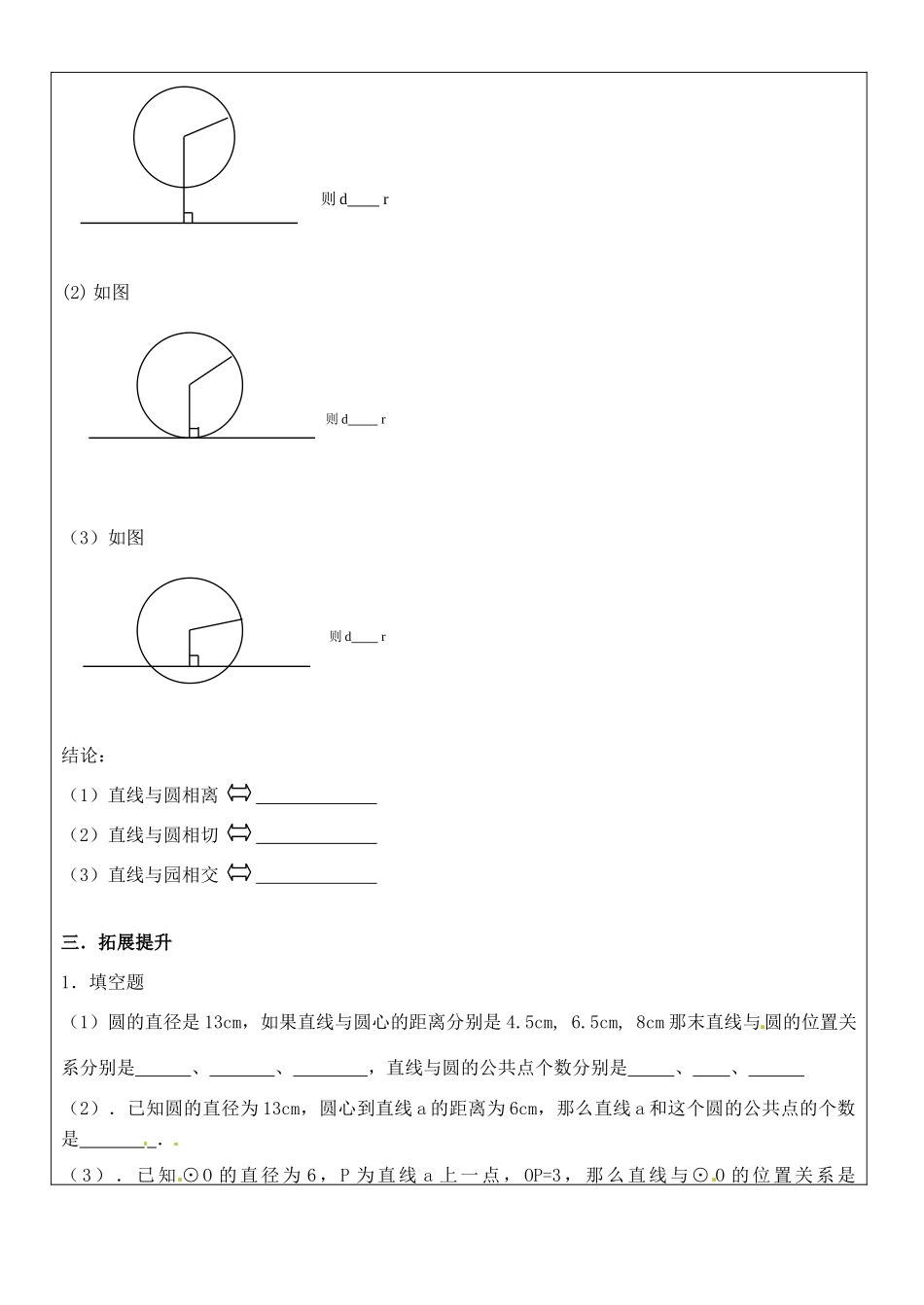
九年级数学上册导学稿课题直线和圆的位置关系(一)课型新授课审核人级部审核讲学时间第四周第2导学稿教师寄语聪明出于勤奋,天才在于积累;好学而不勤问非真好学者。学习目标1.熟练掌握直线和圆的三种位置关系;2.利用直线和圆的三种位置关系解决简单的应用问题。教学重点直线和圆的三种位置关系教学难点直线和圆的三种位置关系的应用教学方法学生自主活动材料一.前置自学1。点与直线的位置关系有种。分别是、、2。⊙O的半径为r,点A到圆心O的距离为d,则(1)点在圆外(2)点在圆上(3)点在圆内二.合作探究1.填空(1)直线和圆没有公共点,称这条直线和圆,这条直线叫做圆的。(2)直线和圆有一个公共点,称这条直线和圆,这条直线叫做圆的。(3)直线和圆有两个公共点,称这条直线和圆,这条直线叫做圆的。2.直线与圆的位置关系的判断设圆的半径为r,直线到圆的距离为d(1)如图(2)如图(3)如图结论:(1)直线与圆相离(2)直线与圆相切(3)直线与园相交三.拓展提升1.填空题(1)圆的直径是13cm,如果直线与圆心的距离分别是4.5cm,6.5cm,8cm那末直线与圆的位置关系分别是、、,直线与圆的公共点个数分别是、、(2).已知圆的直径为13cm,圆心到直线a的距离为6cm,那么直线a和这个圆的公共点的个数是.(3).已知⊙O的直径为6,P为直线a上一点,OP=3,那么直线与⊙O的位置关系是则dr则dr则dr。2.选择题⊙O的半径为R,直线a和⊙O有公共点,若圆心到直线a的距离是d,则d与R的大小关系是()A.d>RB.d<RC.d≥RD.d≤R3.解答题在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?(1)r=2cm;(2)r=2.4cm(3)r=3cm.四.课堂训练1.已知圆的半径为6.5cm,如果一条直线与圆心的距离为6.5cm,那么则条直线和这个圆的位置关系为()A.相交B.相切C.相离D.相交或相离2.半径为R=3cm的与直线a有公共点,且直线a和点O的距离为,则()A.d=3cmB.d<3cmC.d>3cmD.d≤3cm3.已知Rt△ABC的斜边AB=10cm,直角边AC=6cm,圆心为C,半径分别为4cm和6cm的两个⊙C1和⊙C2与AB有怎样的位置关系?半径为多长时,AB与⊙C相切?自我评价专栏(分优良中差四个等级)自主学习:合作与交流:书写:综合: