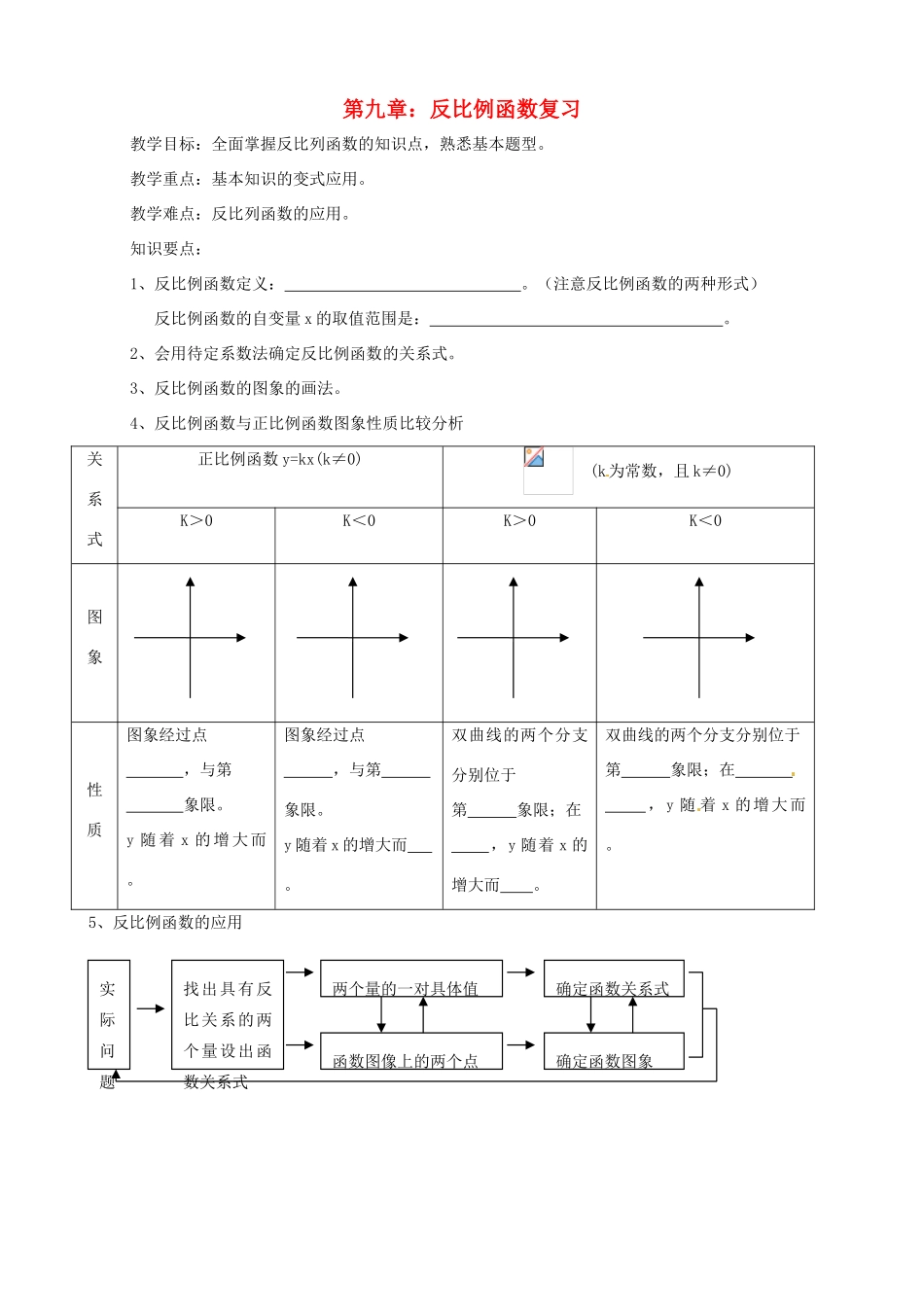
第九章:反比例函数复习教学目标:全面掌握反比列函数的知识点,熟悉基本题型。教学重点:基本知识的变式应用。教学难点:反比列函数的应用。知识要点:1、反比例函数定义:。(注意反比例函数的两种形式)反比例函数的自变量x的取值范围是:。2、会用待定系数法确定反比例函数的关系式。3、反比例函数的图象的画法。4、反比例函数与正比例函数图象性质比较分析关系式正比例函数y=kx(k≠0)(k为常数,且k≠0)K>0K<0K>0K<0图象性质图象经过点,与第象限。y随着x的增大而。图象经过点,与第象限。y随着x的增大而。双曲线的两个分支分别位于第象限;在,y随着x的增大而。双曲线的两个分支分别位于第象限;在,y随着x的增大而。5、反比例函数的应用找出具有反比关系的两个量设出函数关系式实际问题两个量的一对具体值确定函数关系式函数图像上的两个点确定函数图象习题巩固1、已知,是反比例函数,则m.此函数图象在第象限。2、正比例函数y=k1x(k1≠0)和反比例函数y=(k2≠0)的一个交点为(m,n),则另一个交点为_________.3、已知是反比例函数(k≠0)图象上的两点,且<0时,,则k________。4、知点A(x1,y1);B(x2,y2);C(x3,y3)在上,且x1<x2<0<x3;比较y1、y2y3的大小是。5、已知一次函数y=kx+b的图象经过第一、二、三象限,则函数y=的图象在()A.第一、三象限B.第二、四象限C.第三、四象限D.第一、二象限6、函数y=a(x-3)与在同一坐标系中的大致图象是()7、水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何随着时间t变化的.请选择匹配的示意图与容器.8、正比例函数与反比例函数的图象交于A,C两点ABX轴于B,CDX轴于于D,则四边形ABCD的面积()A.1B.C.2D.9、若点(3,4)是反比例函数y=图象上一点,则此函数图象必经过点()A.(2,6)B.(2,-6)C.(4,-3)D.(3,-4)10、如图,已知直线与x轴y轴分别交于点A、B,与双曲线()分别交于点C、D,且C点的坐标为(-1,2)。⑴分别求出直线AB与双曲线的解析式⑵若D点的纵坐标为1,求出点D的坐标;⑶利用图象直接写出当x在什么范围内取值时?11.如图,已知点(1,3)在函数(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数(x>0)的图象又经过A、E两点,点E的横坐标为m(1)求k的值;(2)求点C的横坐标(用m表示);(3)当∠ABD=45°时,求m的值.CBoyADEDACBDACB