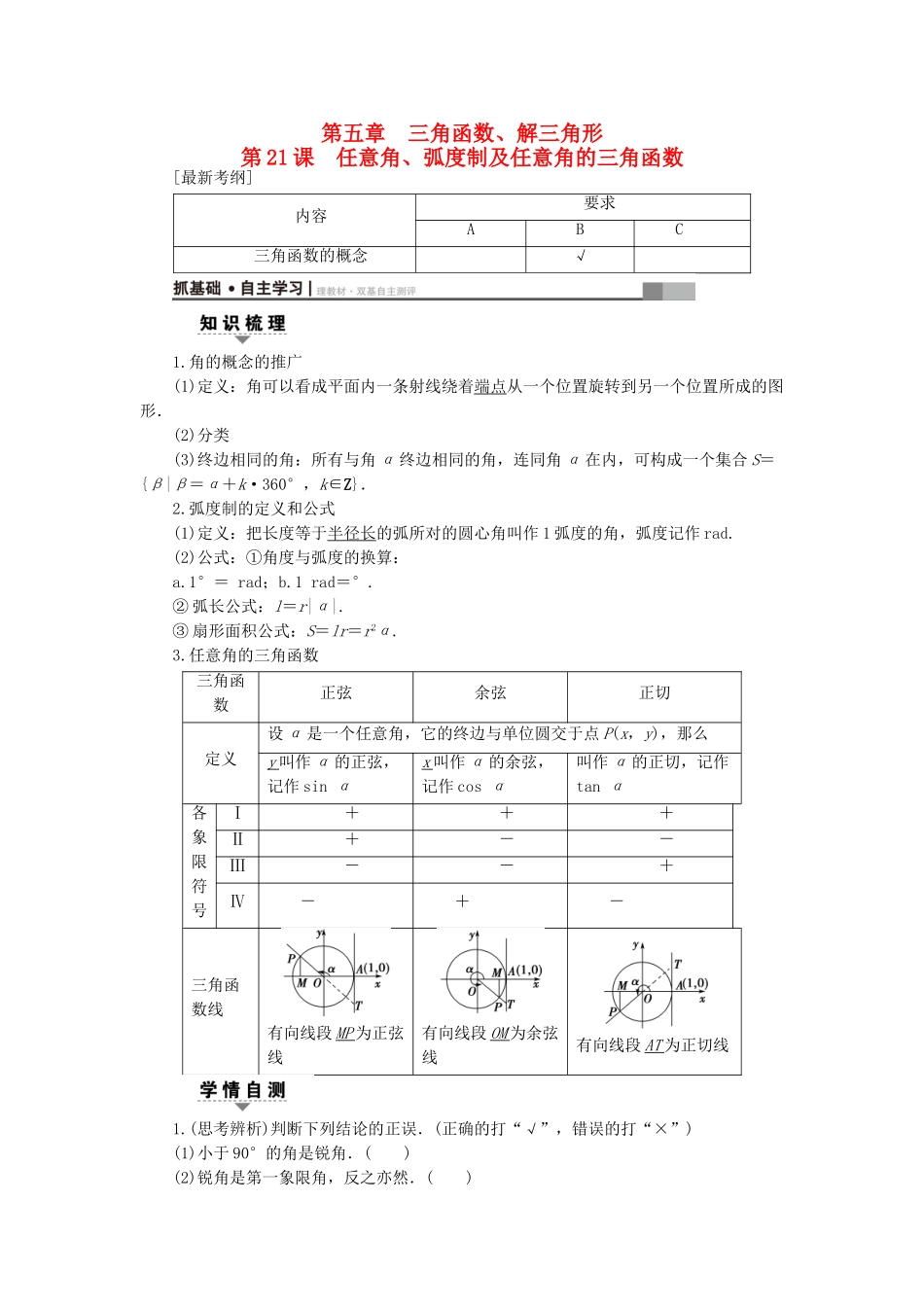
第五章三角函数、解三角形第21课任意角、弧度制及任意角的三角函数[最新考纲]内容要求ABC三角函数的概念√1.角的概念的推广(1)定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.(2)分类(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z}.2.弧度制的定义和公式(1)定义:把长度等于半径长的弧所对的圆心角叫作1弧度的角,弧度记作rad.(2)公式:①角度与弧度的换算:a.1°=rad;b.1rad=°.②弧长公式:l=r|α|.③扇形面积公式:S=lr=r2α.3.任意角的三角函数三角函数正弦余弦正切定义设α是一个任意角,它的终边与单位圆交于点P(x,y),那么y叫作α的正弦,记作sinαx叫作α的余弦,记作cosα叫作α的正切,记作tanα各象限符号Ⅰ+++Ⅱ+--Ⅲ--+Ⅳ-+-三角函数线有向线段MP为正弦线有向线段OM为余弦线有向线段AT为正切线1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)小于90°的角是锐角.()(2)锐角是第一象限角,反之亦然.()(3)角α的三角函数值与终边上点P的位置无关.()(4)若α为第一象限角,则sinα+cosα>1.()[答案](1)×(2)×(3)√(4)√2.(教材改编)已知角α的终边与单位圆的交点为M,则sinα=________.±[由题意知|r|2=2+y2=1,所以y=±.由三角函数定义知sinα=y=±.]3.若cosθ>0,且sin2θ<0,则角θ的终边在第________象限.四[由cosθ>0,sin2θ=2sinθcosθ<0得sinθ<0,则角θ的终边在第四象限.]4.在单位圆中,200°的圆心角所对的弧长为________.π[单位圆的半径r=1,200°的弧度数是200×=π,由弧度数的定义得π=,所以l=π.]5.已知半径为120mm的圆上,有一条弧长是144mm,则该弧所对的圆心角的弧度数为________rad.1.2[由题意知α===1.2rad.]角的有关概念及其集合表示(1)若角α是第二象限角,则是第________象限角.【导学号:62172118】(2)已知角α的终边在如图211所示阴影部分表示的范围内(不包括边界),则角α用集合可表示为________.图211(1)一或三(2)(k∈Z)[(1) α是第二象限角,∴+2kπ<α<π+2kπ,k∈Z,∴+kπ<<+kπ,k∈Z.当k为偶数时,是第一象限角;当k为奇数时,是第三象限角.综上,是第一或第三象限角.(2)在[0,2π)内,终边落在阴影部分角的集合为,∴所求角的集合为(k∈Z).][规律方法]1.与角α终边相同的角可以表示为β=2kπ+α(k∈Z)的形式,α是任意角;相等的角终边一定相同,终边相同的角不一定相等;角度制与弧度制不能混用.2.由α所在象限,判定所在象限,应先确定的范围,并对整数k的奇、偶情况进行讨论.[变式训练1]已知角α=45°,在区间[-720°,0°]内与角α有相同终边的角β=________.-675°或-315°[由终边相同的角的关系知β=k·360°+45°,k∈Z,∴取k=-2,-1,得β=-675°或β=-315°.]扇形的弧长、面积公式(1)已知扇形周长为10,面积是4,求扇形的圆心角;(2)已知扇形周长为40,当它的半径和圆心角分别取何值时,扇形的面积最大?【导学号:62172119】[解](1)设圆心角是θ,半径是r,则解得(舍去)或∴扇形的圆心角为.(2)设圆心角是θ,半径是r,则2r+rθ=40.又S=θr2=r(40-2r)=r(20-r)=-(r-10)2+100≤100.当且仅当r=10时,Smax=100,此时2×10+10θ=40,θ=2,∴当r=10,θ=2时,扇形的面积最大.[规律方法]1.(1)在弧度制下,计算扇形面积和弧长比在角度制下更方便、简捷;(2)从扇形面积出发,在弧度制下把问题转化为关于R的二次函数的最值问题(如本例)或不等式问题来求解.2.利用公式:(1)l=αR;(2)S=lR;(3)S=αR2.其中R是扇形的半径,l是弧长,α(0<α<2π)为圆心角,S是扇形面积,知道两个量,可求其余量.[变式训练2]若扇形的圆心角α=120°,弦长AB=12cm,则弧长l=________cm.π[设扇形的半径为rcm,如图.由sin60°=,得r=4cm,∴l=|α|·r=×4=πcm.]三角函数的定义(1)若tanα>0,则下列说法正确的是________.(填序号)①sinα>0;②cosα>0;③sin2α>0;④cos2α>0.(2)已知角α的终边经过点A(-...