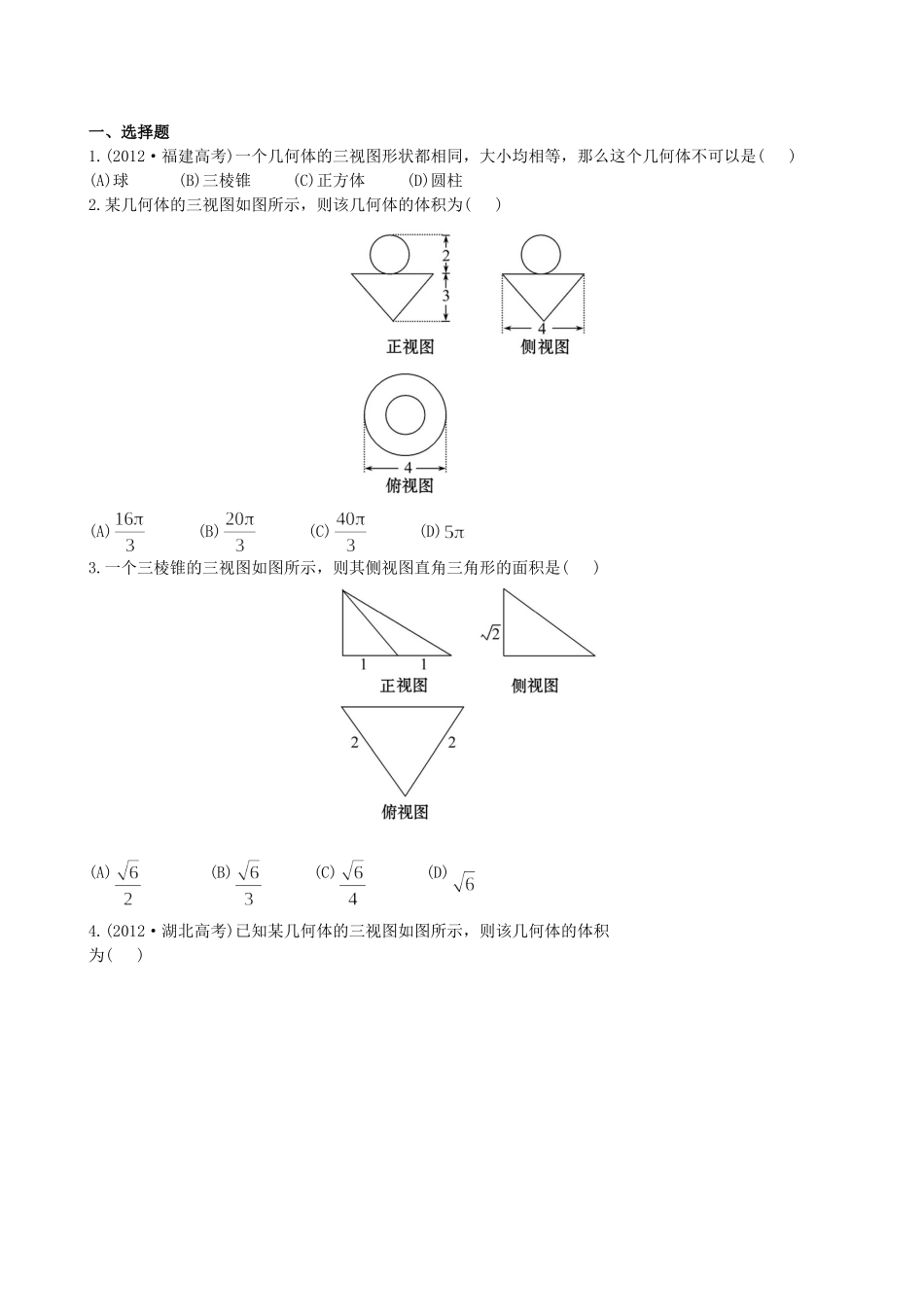
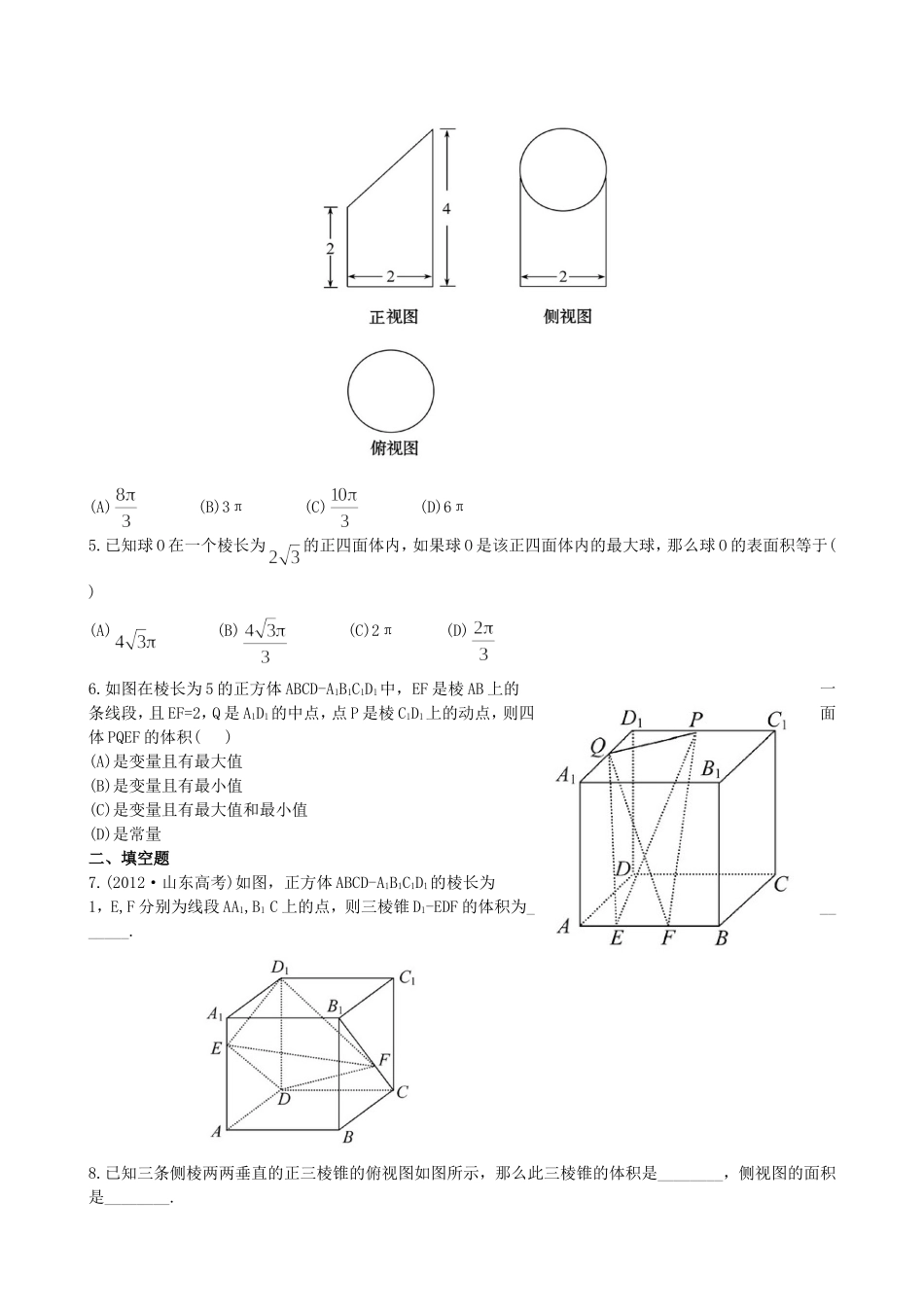
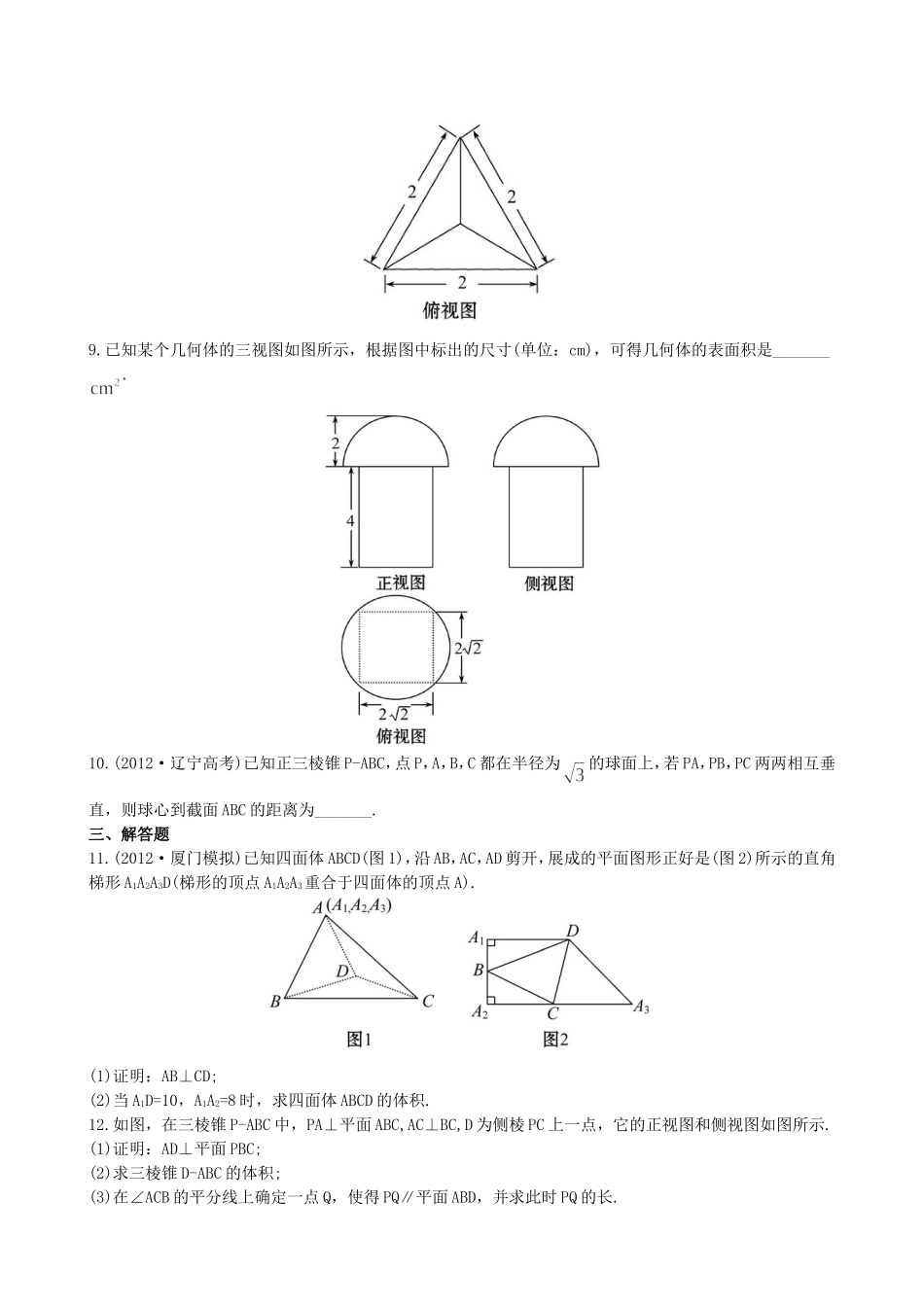
一、选择题1.(2012·福建高考)一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是()(A)球(B)三棱锥(C)正方体(D)圆柱2.某几何体的三视图如图所示,则该几何体的体积为()(A)(B)(C)(D)3.一个三棱锥的三视图如图所示,则其侧视图直角三角形的面积是()(A)(B)(C)(D)4.(2012·湖北高考)已知某几何体的三视图如图所示,则该几何体的体积为()(A)(B)3π(C)(D)6π5.已知球O在一个棱长为的正四面体内,如果球O是该正四面体内的最大球,那么球O的表面积等于()(A)(B)(C)2π(D)6.如图在棱长为5的正方体ABCD-A1B1C1D1中,EF是棱AB上的一条线段,且EF=2,Q是A1D1的中点,点P是棱C1D1上的动点,则四面体PQEF的体积()(A)是变量且有最大值(B)是变量且有最小值(C)是变量且有最大值和最小值(D)是常量二、填空题7.(2012·山东高考)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.8.已知三条侧棱两两垂直的正三棱锥的俯视图如图所示,那么此三棱锥的体积是________,侧视图的面积是________.9.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得几何体的表面积是_______.10.(2012·辽宁高考)已知正三棱锥P-ABC,点P,A,B,C都在半径为的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为_______.三、解答题11.(2012·厦门模拟)已知四面体ABCD(图1),沿AB,AC,AD剪开,展成的平面图形正好是(图2)所示的直角梯形A1A2A3D(梯形的顶点A1A2A3重合于四面体的顶点A).(1)证明:AB⊥CD;(2)当A1D=10,A1A2=8时,求四面体ABCD的体积.12.如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正视图和侧视图如图所示.(1)证明:AD⊥平面PBC;(2)求三棱锥D-ABC的体积;(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.答案解析1.【解析】选D.球、正方体的三视图形状都相同,大小均相等,首先排除A和C,对于如图所示的三棱锥O-ABC,当OA,OB,OC两两垂直且OA=OB=OC时,其三视图的形状都相同,大小均相等,故排除选项B,而不论圆柱如何放置,其三视图的形状都不会完全相同,故选D.2.【解析】选A.此几何体是由一个球体和一个锥体组合而成的,球体的半径为1,圆锥体的底面半径为2,高为3,由体积计算公式知3.【解析】选A.由正视图和俯视图可知,该几何体的底面是边长为2的正三角形,即俯视图为边长为2的正三角形,故侧视图的另一条直角边长为所以S侧=4.【解析】选B.由三视图可知,此几何体是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的则可在其上部补上一个与它完全相同的几何体,得【方法技巧】不规则或较复杂几何体的体积的求解技巧(1)补体法:把不规则(不熟悉或复杂)的几何体延伸或补成规则的(熟悉的或简单的)可用公式求解的几何体,从而求解.(2)割体法:把复杂(不规则)的几何体切割成可用公式求解的(规则的)几何体.(3)等积法:把几何体的体积通过已知条件转化为易求体积的几何体求解.5.【解析】选C.由题意可知,球O是棱长为的正四面体的内切球,易求内切球的半径r=∴S表面积=6.【解析】选D.因为点Q到直线EF的距离为定值|QA|,且EF的长度为定值,所以△QEF的面积为定值;又因为D1C1∥AB,故D1C1∥平面QEF,P点到QEF的距离也为定值.综上,四面体PQEF的体积为定值.7.【解析】△DED1的面积为正方形面积的一半,若△DED1为所求三棱锥的底面,则三棱锥的高等于正方体的棱长,所以=答案:8.【解析】由已知,该三棱锥如图所示:则V==该三棱锥的侧视图为△PDC,其中△PDC的高PO==于是侧视图面积为S=答案:9.【解析】由三视图可知几何体为四棱柱及其上方有一半径为2的半球,其中四棱柱的底面是边长为的正方形,侧棱长为4,故其表面积S=答案:10.【解析】如图,设PA=a,则设球的半径为R,则有将R=代入上式,解得a=2,a=0(舍)∴所求距离为答案:11.【解析】(1)在四面体ABCD中,⇒AB⊥面ACD⇒AB⊥CD.(2)在题图2中作DE⊥A2A3于E. A1A2=8,∴DE=8.又 A1D=A3D=10,∴EA3=6,A2A3=10+6=16.又A2C=A3C,∴A2C=8,即题图1中AC=8,AD=10,由A1A2=8,A1B=A2B得题图1中AB=4,∴S△ACD==32.又 AB⊥面ACD,∴VB-AC...