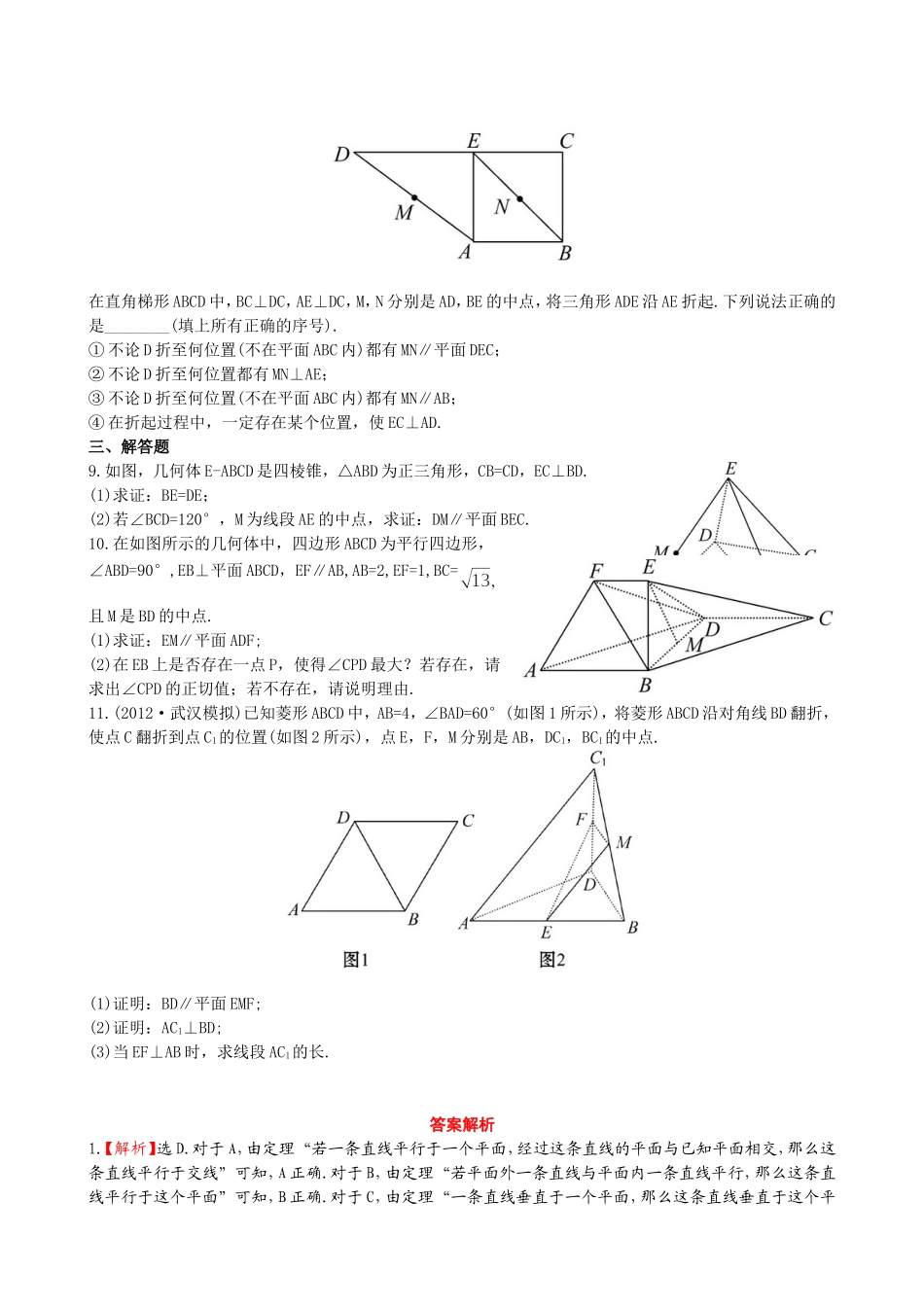
一、选择题1.已知平面α∩β=l,m是α内不同于l的直线,那么下列命题中错误的是()(A)若m∥β,则m∥l(B)若m∥l,则m∥β(C)若m⊥β,则m⊥l(D)若m⊥l,则m⊥β2.设m,n是两条不同的直线,α,β,γ是三个不同的平面,有下列四个命题:①若m⊂β,α⊥β,则m⊥α;②若α∥β,m⊂α,则m∥β;③若n⊥α,n⊥β,m⊥α,则m⊥β;④若α⊥γ,β⊥γ,m⊥α,则m⊥β.其中正确命题的序号是()(A)①③(B)①②(C)③④(D)②③3.(2012·四川高考)下列命题正确的是()(A)若两条直线和同一个平面所成的角相等,则这两条直线平行(B)若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行(C)若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行(D)若两个平面都垂直于第三个平面,则这两个平面平行4.已知直线m⊂平面α,则“平面α∥平面β”是“m∥β”的()(A)充要条件(B)充分不必要条件(C)必要不充分条件(D)既不充分也不必要条件5.(2012·浙江高考)已知矩形ABCD,AB=1,BC=将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中()(A)存在某个位置,使得直线AC与直线BD垂直(B)存在某个位置,使得直线AB与直线CD垂直(C)存在某个位置,使得直线AD与直线BC垂直(D)对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直二、填空题6.(2012·咸宁模拟)如图,在正方体ABCD-A1B1C1D1中,M,N分别是棱C1D1,C1C的中点.以下四个结论:①直线AM与直线CC1相交;②直线AM与直线BN平行;③直线AM与直线DD1异面;④直线BN与直线MB1异面.其中正确结论的序号为_______(注:把你认为正确的结论序号都填上).7.(2012·鄂州模拟)设x,y,z是空间中的不同直线或不同平面,下列条件中能保证“若x⊥z,且y⊥z,则x∥y”为真命题的是________(填出所有正确条件的代号).①x为直线,y,z为平面;②x,y,z为平面;③x,y为直线,z为平面;④x,y为平面,z为直线;⑤x,y,z为直线.8.(2012·十堰模拟)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起.下列说法正确的是________(填上所有正确的序号).①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;②不论D折至何位置都有MN⊥AE;③不论D折至何位置(不在平面ABC内)都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.三、解答题9.如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.10.在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,BC=且M是BD的中点.(1)求证:EM∥平面ADF;(2)在EB上是否存在一点P,使得∠CPD最大?若存在,请求出∠CPD的正切值;若不存在,请说明理由.11.(2012·武汉模拟)已知菱形ABCD中,AB=4,∠BAD=60°(如图1所示),将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.(1)证明:BD∥平面EMF;(2)证明:AC1⊥BD;(3)当EF⊥AB时,求线段AC1的长.答案解析1.【解析】选D.对于A,由定理“若一条直线平行于一个平面,经过这条直线的平面与已知平面相交,那么这条直线平行于交线”可知,A正确.对于B,由定理“若平面外一条直线与平面内一条直线平行,那么这条直线平行于这个平面”可知,B正确.对于C,由定理“一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线”可知,C正确.对于D,若一条直线与一个平面内的一条直线垂直,这条直线未必垂直于这个平面,因此D不正确.综上所述,选D.2.【解析】选D.若m⊂β,α⊥β,则m∥α或m与α相交或m⊂α,故①错误;若α∥β,m⊂α,则m与β没有公共点,所以m∥β,故②正确;若n⊥α,n⊥β,则α∥β,又 m⊥α,∴m⊥β,故③正确;若α⊥γ,β⊥γ,则α与β可平行、可相交(可垂直),故④错误;即正确的命题为②③.3.【解析】选C.4.【解析】选B.由直线m⊂平面α,平面α∥平面β,可知m与β无公共点,所以m∥β.由m⊂平面α,m∥β,则平面α可能平行于平面β,也可能与平面β相交,所以应选B.5.【解析】选B.分别取AD,AC,BC的中点E,F,G,则EF∥CD,FG∥AB,且...