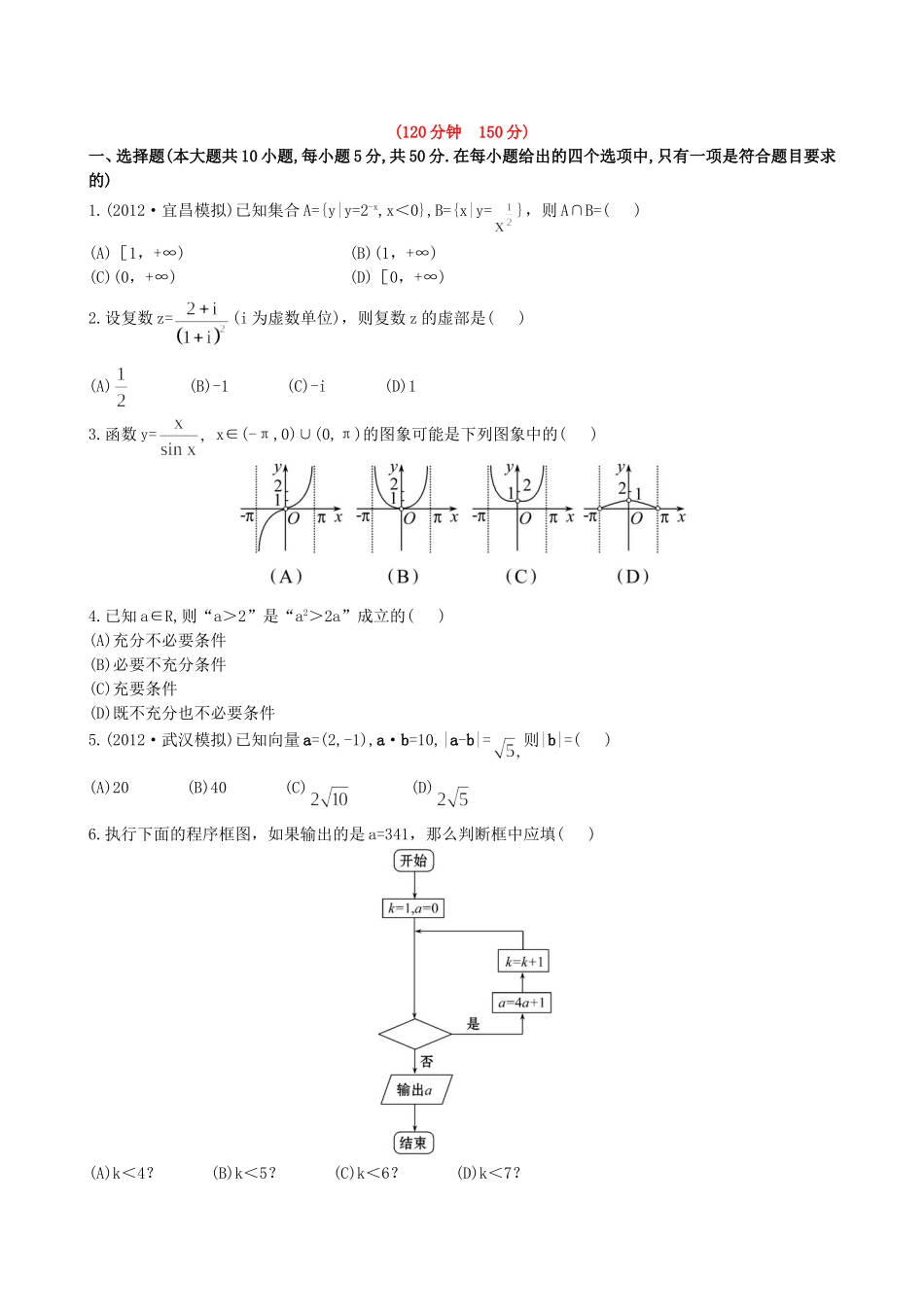
(120分钟150分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2012·宜昌模拟)已知集合A={y|y=2-x,x<0},B={x|y=},则A∩B=()(A)[1,+∞)(B)(1,+∞)(C)(0,+∞)(D)[0,+∞)2.设复数z=(i为虚数单位),则复数z的虚部是()(A)(B)-1(C)-i(D)13.函数y=x∈(-π,0)∪(0,π)的图象可能是下列图象中的()4.已知a∈R,则“a>2”是“a2>2a”成立的()(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件5.(2012·武汉模拟)已知向量a=(2,-1),a·b=10,|a-b|=则|b|=()(A)20(B)40(C)(D)6.执行下面的程序框图,如果输出的是a=341,那么判断框中应填()(A)k<4?(B)k<5?(C)k<6?(D)k<7?7.由直线x=x=y=0与曲线y=cosx所围成的封闭图形的面积为()(A)(B)1(C)(D)8.(2012·广东高考)已知变量x,y满足约束条件则z=3x+y的最大值为()(A)12(B)11(C)3(D)-19.(2012·荆州模拟)已知函数f(x+1)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式(x1-x2)[f(x1)-f(x2)]<0恒成立,则不等式f(1-x)<0的解集为()(A)(1,+∞)(B)(-∞,0)(C)(0,+∞)(D)(-∞,1)10.设f(x)是R上的可导函数,且满足f′(x)>f(x),对任意的正实数a,下列不等式恒成立的是()(A)f(a)eaf(0)(C)f(a)<(D)f(a)>二、填空题(本大题共5小题,每小题5分,共25分.请把正确的答案填在题中的横线上)11.(2012·孝感模拟)已知2a-b=(-1,),c=(1,),且a·c=3,|b|=4,则b与c的夹角为______.12.已知函数f(x)=则不等式f(x)>0的解集为______.13.已知函数f(x)=+lnx-2x在定义域内是增函数,则实数m的取值范围为_______.14.定义在R上的函数f(x)满足f(x)=则f(2013)=______.15.(2012·济南模拟)下列正确命题的序号是________.(1)“m=-2”是直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直的必要不充分条件;(2)a∈R,使得函数y=|x+1|+|x+a|是偶函数;(3)不等式:≥由此猜测第n个不等式为(4)若二项式的展开式中所有项的系数之和为243,则展开式中x-4的系数是40.三、解答题(本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤)16.(12分)已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y=0≤x≤3}.(1)若A∩B=,求a的取值范围;(2)当a取使不等式x2+1≥ax恒成立的a的最小值时,求()∩B.17.(12分)(2012·宁德模拟)已知函数f(x)=2x+k·2-x,k∈R.(1)若函数f(x)为奇函数,求实数k的值;(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.18.(12分)设f(x)=g(x)=ax+5-2a(a>0).(1)求f(x)在x∈[0,1]上的值域;(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.19.(12分)(2012·杭州模拟)已知a∈R,函数f(x)=+lnx-1,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在区间(0,e]上的单调性;(2)是否存在实数x0∈(0,e],使曲线y=g(x)在点x=x0处的切线与y轴垂直?若存在,求出x0的值;若不存在,请说明理由.20.(13分)某地建一座桥,两端的桥墩已建好,这两桥墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元,距离为x米的相邻两桥墩之间的桥面工程费用为(2+)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记余下工程的费用为y万元.(1)试写出y关于x的函数关系式;(2)当m=640米时,需新建多少个桥墩才能使y最小?21.(14分)已知函数f(x)=px--2lnx,g(x)=(1)若p=2,求曲线f(x)在点(1,f(1))处的切线方程;(2)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;(3)若p2-p≥0,且至少存在一点x0∈[1,e],使得f(x0)>g(x0)成立,求实数p的取值范围.答案解析1.【解析】选B.集合A=(1,+∞),B=[0,+∞),故答案为B.2.【解析】选B.z=故复数z的虚部是-1.3.【解析】选C.因函数y=是偶函数,故排除A,又x∈(0,)时,x>sinx,即>1,排除B,D,故选C.4.【解析】选A.a>2可以推出a2>2a;a2>2a可以推出a>2或a<0,不一定推出a>2.“a>2”是“a2>2a”成立的充分不必要条件.5.【解析】选D.|a-b|=解得|b|=6.【解析】选C.由程序框图知k=1时,执行第一...