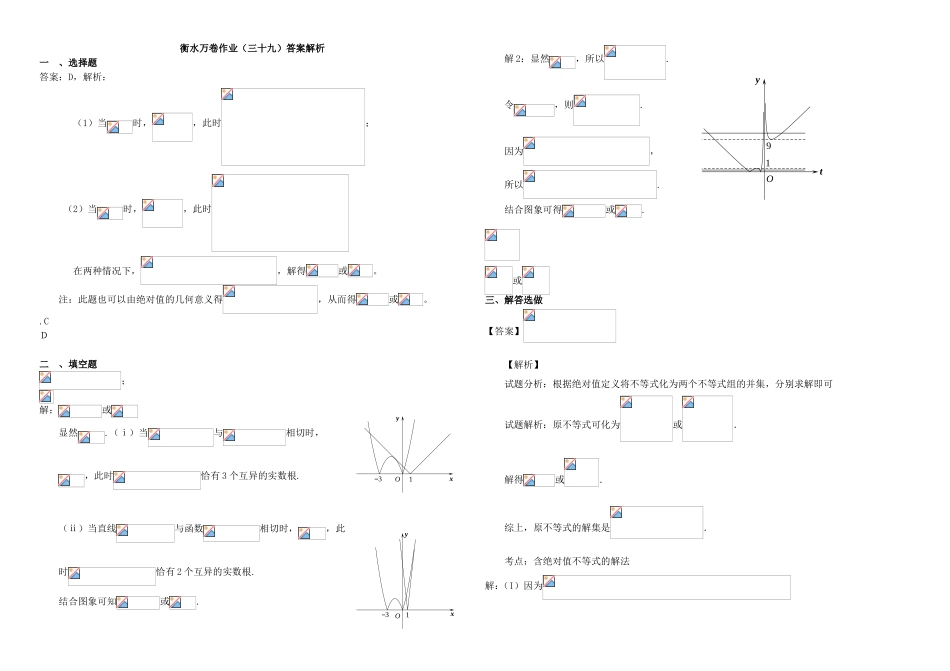
衡水万卷作业(三十九)不等式选讲考试时间:45分钟姓名:__________班级:__________考号:__________题号一二三总分得分一、选择题(本大题共3小题,每小题5分,共15分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)若函数的最小值为3,则实数的值为()A.5或8B.或5C.或D.或8(1).(不等式选做题)对任意,的最小值为()A.B.C.D.记,,设a,b为平面向量,则()A.B.C.D.二、填空题(本大题共5小题,每小题5分,共25分)不等式的解集为。若关于的不等式的解集为,则已知函数,.若方程恰有4个互异的实数根,则实数的取值范围为__________.若不等式对任意实数恒成立,则实数的取值范围是____________.已知函数,,若对任意的,都有成立,则实数的取值范围为.三、解答选做(本大题共4小题,共60分)(选修4—5:不等式选讲)解不等式选修4-5:不等式选讲设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd;则;(2)是的充要条件。试题分析:(I)由及,可证明,开方即得.(II)本小题可借助第一问的结论来证明,但要分必要性与充分性来证明.已知函数(1)解不等式(2)若存在实数x,使得,求实数a的取值范围,选修4-5:不等式选讲若,且,求的最小值.衡水万卷作业(三十九)答案解析一、选择题答案:D,解析:(1)当时,,此时;(2)当时,,此时在两种情况下,,解得或。注:此题也可以由绝对值的几何意义得,从而得或。.CD二、填空题;解:或显然.(ⅰ)当与相切时,,此时恰有3个互异的实数根.(ⅱ)当直线与函数相切时,,此时恰有2个互异的实数根.结合图象可知或.解2:显然,所以.令,则.因为,所以.结合图象可得或.或三、解答选做【答案】【解析】试题分析:根据绝对值定义将不等式化为两个不等式组的并集,分别求解即可试题解析:原不等式可化为或.解得或.综上,原不等式的解集是.考点:含绝对值不等式的解法解:(I)因为xy31Oxy13OtyO91由题设a+b=c+d,ab>cd,得,因此(2)(i)若,则,即,因为a+b=c+d,所以ab>cd,由(1)得,(ii)若,则,即,因为a+b=c+d,所以ab>cd,于是,因此。综上,是的充要条件考点:不等式证明.(1)①当时,,所以②当时,,所以为③当时,,所以综合①②③不等式的解集为(2)即由绝对值的几何意义,只需【答案】解析:因为,所以,又因为,所以,且当时取等号.所以,且当时取等号.所以的最小值为.【思路点拨】先由,得到,结合已知条件得,然后利用基本不等式可求出结论.