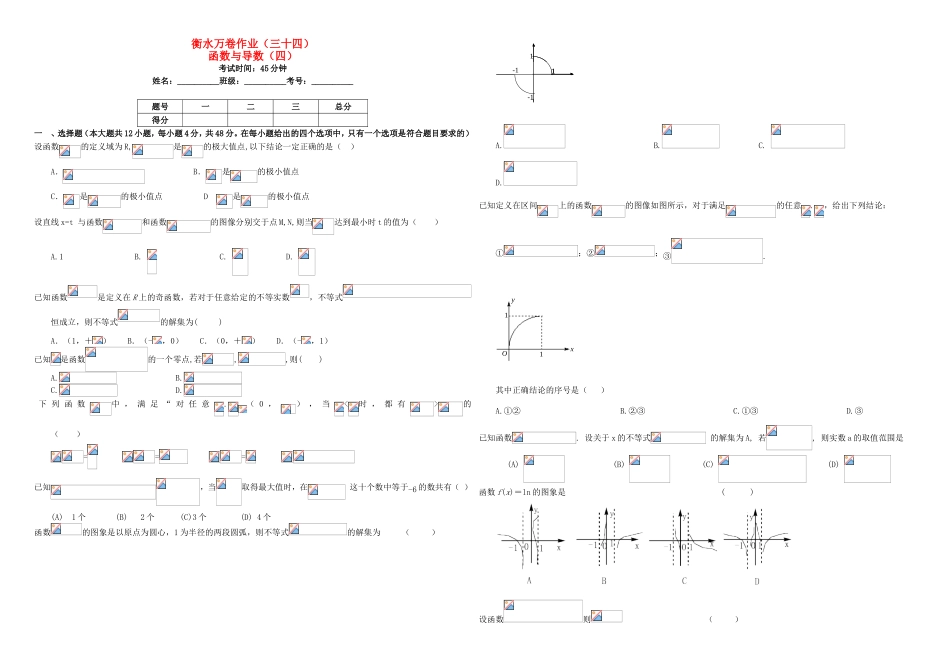
衡水万卷作业(三十四)函数与导数(四)考试时间:45分钟姓名:__________班级:__________考号:__________题号一二三总分得分一、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)设函数的定义域为R,是的极大值点,以下结论一定正确的是()A.B.是的极小值点C.是的极小值点D是的极小值点设直线x=t与函数和函数的图像分别交于点M,N,则当达到最小时t的值为()A.1B.C.D.已知函数是定义在R上的奇函数,若对于任意给定的不等实数,不等式恒成立,则不等式的解集为()A.(1,+)B.(-,0)C.(0,+)D.(-,1)已知是函数的一个零点,若,,则()A.B.C.D.下列函数中,满足“对任意.(0,),当<时,都有>的()===已知,当取得最大值时,在这十个数中等于-6的数共有()(A)1个(B)2个(C)3个(D)4个函数的图象是以原点为圆心,1为半径的两段圆弧,则不等式的解集为()-111-1-111-1A.B.C.D.已知定义在区间上的函数的图像如图所示,对于满足的任意.,给出下列结论:①;②;③.yxO11其中正确结论的序号是()A.①②B.②③C.①③D.③已知函数.设关于x的不等式的解集为A,若,则实数a的取值范围是(A)(B)(C)(D)函数f(x)=ln的图象是()设函数则()A.在区间内均有零点B.在区间内均无零点C.在区间内有零点,在区间内无零点D.在区间内无零点,在区间内有零点定义区间,,,的长度均为,多个区间并集的长度为各区间长度之和,例如,的长度.用表示不超过的最大整数,记,其中.设,,若用分别表示不等式,方程,不等式解集区间的长度,则当时,有()(A)(B)(C)(D)二、填空题(本大题共6小题,每小题4分,共24分)已知f(x)=x|x﹣1|+1,f(2x)=(其中x>0),则x=.有下列说法:①用二分法研究函数的近似解时,第一次经计算,第二次应计算;②函数的零点所在大致区间;③对于函数,若,则函数在内至多有一个零点;④或;有两个不同的零点,则是的充要条件,其中说法正确的是(将所有正确说法的序号全部填在横线上).已知函数则方程恰有两个不同的实根时,实数的取值范围是_______________.设函数,记,若函数至少存在一个零点,则实数的取值范围是.已知,若的零点个数不为,则的最小值为.若函数()满足且时,,函数,则函数在区间内零点的个数有___个.三、解答题(本大题共2小题,共28分)19.已知函数().(1)当时,求函数的单调区间;(2)当时,取得极值.①若,求函数在上的最小值;②求证:对任意,都有.20.已知函数()=,g()=+。(1)求函数h()=()-g()的零点个数。并说明理由;(2)设数列{}()满足,,证明:存在常熟M,使得对于任意的,都有≤.衡水万卷作业(三十四)答案解析一、选择题CDBB【解析】由于函数在上单调递增函数在上单调递增,故函数在上单调递增,所以函数在上只有唯一的零点,所以在上,在上.ACCBABDB二、填空题考点:函数的值.专题:函数的性质及应用.分析:由已知得,由此能求出.解答: f(x)=x|x﹣1|+1,f(2x)=(其中x>0),∴,∴, x>0,∴(2x)2﹣2x﹣=0,解得2x=,∴.故答案为:.点评:本题考查函数值的求法及应用,是基础题,解题时要注意函数性质的合理运用.①②④.112三、解答题解:(1)当时,解得或,解得所以单调增区间为和,单调减区间为(2)①当时,取得极值,所以解得(经检验符合题意)+0-0+↗↘↗所以函数在,递增,在递减当时,在单调递减,当时在单调递减,在单调递增,当时,在单调递增,综上,在上的最小值②令得(舍)因为所以所以,对任意,都有解析:(I)由知,,而,且,则为的一个零点,且在内有零点,因此至少有两个零点解法1:,记,则。当时,,因此在上单调递增,则在内至多只有一个零点。又因为,则在内有零点,所以在内有且只有一个零点。记此零点为,则当时,;当时,;所以,当时,单调递减,而,则在内无零点;当时,单调递增,则在内至多只有一个零点;从而在内至多只有一个零点。综上所述,有且只有两个零点。解法2:,记,则。当时,,因此在上单调递增,则在内至多只有一个零点。因此在内也至多只有一个零点,综上所述,有且只有两个零点。(II)记的正零点为,即。(1)当时,由,即.而,因此...