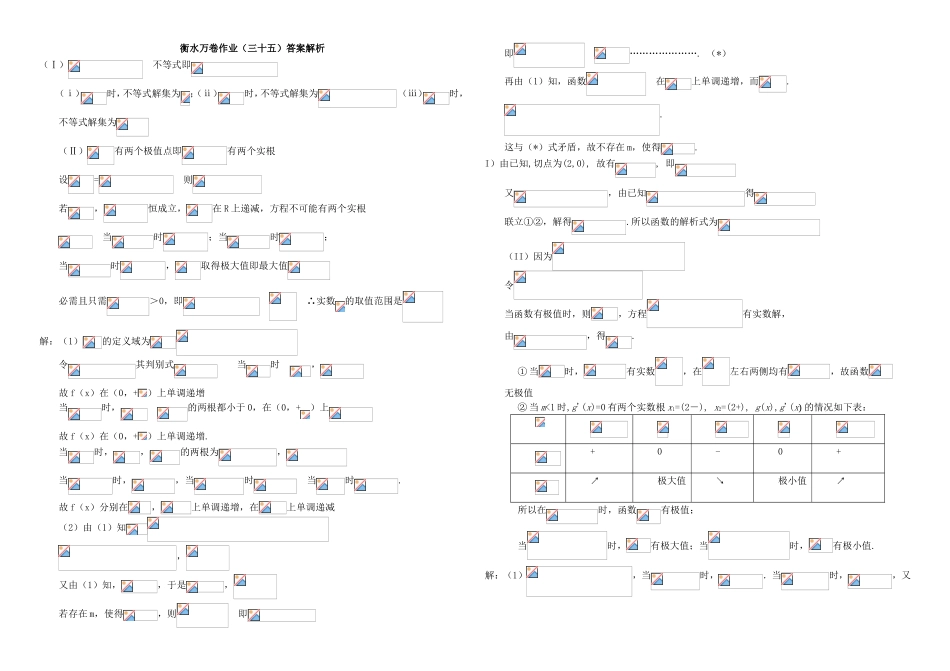
衡水万卷作业(三十五)函数与导数(五)考试时间:45分钟姓名:__________班级:__________考号:__________一、解答题(本大题共5小题,共100分)已知函数(,为自然对数的底数),是的导函数.(I)解关于的不等式>;(II)若有两个极值点,求实数的取值范围.设函数.(1)讨论的单调性.(2)若有两个极值是和,过点,的直线的斜率为,问:是否存在,使得?若存在,求出的值,若不存在,请说明理由.已知函数的图象在与轴交点处的切线方程是.(I)求函数的解析式;(II)设函数,若的极值存在,求实数的取值范围以及函数取得极值时对应的自变量的值.已知函数(为实常数).(1)当时,求函数在上的最大值及相应的值;(2)当时,讨论方程根的个数.(3)若,且对任意的,都有,求实数a的取值范围.已知函数,(1)判断函数的奇偶性;(2)求函数的单调区间;(3)若关于的方程有实数解,求实数的取值范围.衡水万卷作业(三十五)答案解析(Ⅰ)不等式即(ⅰ)时,不等式解集为;(ⅱ)时,不等式解集为(ⅲ)时,不等式解集为(Ⅱ)有两个极值点即有两个实根设=则若,恒成立,在R上递减,方程不可能有两个实根当时;当时;当时,取得极大值即最大值必需且只需>0,即∴实数的取值范围是解:(1)的定义域为令其判别式当时,故f(x)在(0,+)上单调递增当时,的两根都小于0,在(0,+)上故f(x)在(0,+)上单调递增.当时,,的两根为,当时,,当时当时.故f(x)分别在,上单调递增,在上单调递减(2)由(1)知,又由(1)知,,于是,若存在m,使得,则即即………………….(*)再由(1)知,函数在上单调递增,而..这与(*)式矛盾,故不存在m,使得.I)由已知,切点为(2,0),故有,即又,由已知得联立①②,解得.所以函数的解析式为(II)因为令当函数有极值时,则,方程有实数解,由,得.①当时,有实数,在左右两侧均有,故函数无极值②当m<1时,g'(x)=0有两个实数根x1=(2-),x2=(2+),g(x),g'(x)的情况如下表:+0-0+↗极大值↘极小值↗所以在时,函数有极值;当时,有极大值;当时,有极小值.解:(1),当时,.当时,,又,故,当时,取等号(2)易知,故,方程根的个数等价于时,方程根的个数。设=,当时,,函数递减,当时,,函数递增。又,,作出与直线的图像,由图像知:当时,即时,方程有2个相异的根;当或时,方程有1个根;当时,方程有0个根;(3)当时,在时是增函数,又函数是减函数,不妨设,则等价于即,故原题等价于函数在时是减函数,恒成立,即在时恒成立。在时是减函数解:(1)函数的定义域为且关于坐标原点对称.为偶函数.(2)当时,令令所以可知:当时,单调递减,当时,单调递增,又因为是偶函数,所以在对称区间上单调性相反,所以可得:当时,单调递增,当时,单调递减,综上可得:的递增区间是:,;的递减区间是:,(3)由,即,显然,可得:令,当时,显然,当时,,单调递减,当时,,单调递增,时,又,所以可得为奇函数,所以图像关于坐标原点对称所以可得:当时,-∴的值域为∴的取值范围是.