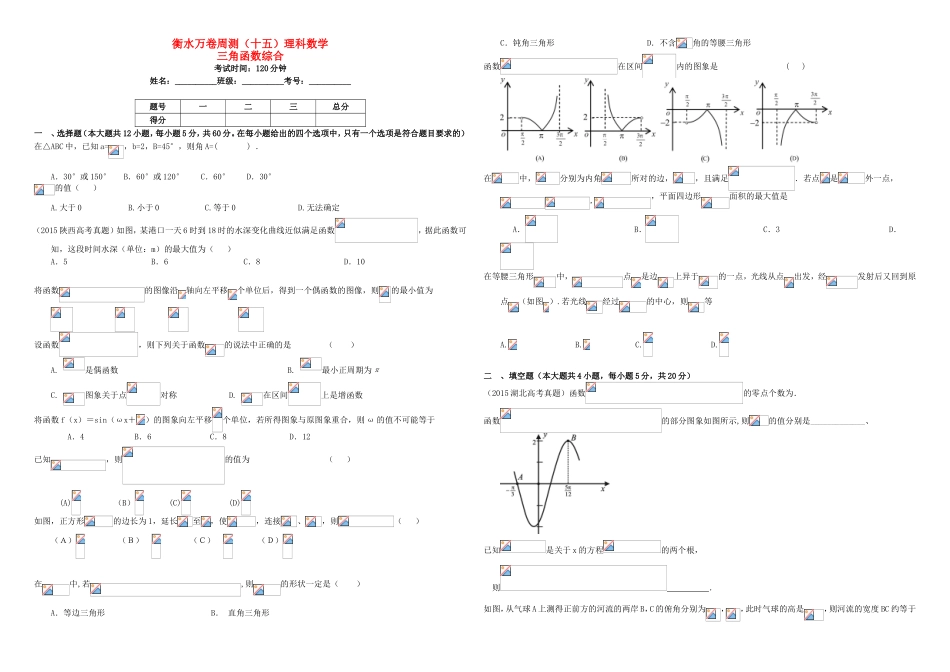
衡水万卷周测(十五)理科数学三角函数综合考试时间:120分钟姓名:__________班级:__________考号:__________题号一二三总分得分一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)在△ABC中,已知a=,b=2,B=45°,则角A=().A.30°或150°B.60°或120°C.60°D.30°的值()A.大于0B.小于0C.等于0D.无法确定(2015陕西高考真题)如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为()A.5B.6C.8D.10将函数的图像沿轴向左平移个单位后,得到一个偶函数的图像,则的最小值为设函数,则下列关于函数的说法中正确的是()A.是偶函数B.最小正周期为πC.图象关于点对称D.在区间上是增函数将函数f(x)=sin(ωx+)的图象向左平移个单位,若所得图象与原图象重合,则ω的值不可能等于A.4B.6C.8D.12已知,则的值为()(A)(B)(C)(D)如图,正方形的边长为1,延长至,使,连接、,则()(A)(B)(C)(D)在中,若,则的形状一定是()A.等边三角形B.直角三角形C.钝角三角形D.不含角的等腰三角形函数在区间内的图象是()在中,分别为内角所对的边,,且满足.若点是外一点,,,平面四边形面积的最大值是A.B.C.3D.在等腰三角形中,点是边上异于的一点,光线从点出发,经发射后又回到原点(如图).若光线经过的中心,则等A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)(2015湖北高考真题)函数的零点个数为.函数的部分图象如图所示,则的值分别是_____________、已知是关于x的方程的两个根,则.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为,,此时气球的高是,则河流的宽度BC约等于。(用四舍五入法将结果精确到个位。参考数据:,,,,)三、解答题(本大题共6小题,第1题10分,后5题12分,共70分)已知a,b,c分别为三个内角A,B,C的(I)求角A的大小;(II)若cosB是方程的值。(2015•丽水一模)在△ABC中,内角A,B,C的对边分别为a,b,c,已知(sinB﹣cosB)(sinC﹣cosC)=4cosBcosC.(Ⅰ)求角A的大小;(Ⅱ)若sinB=psinC,且△ABC是锐角三角形,求实数p的取值范围.已知函数为偶函数,且其图象上相邻两对称轴之间的距离为。(Ⅰ)求函数的表达式;(Ⅱ)若,求的值.已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN=π,在△ABC中,角A、B、C所对的边分别是a、b、c.(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;(Ⅱ)若c=,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.在△ABC中,角A,B,C所对的边分别为,b,c,且,=1,b=2。(1)求∠C和边c;(2)若,,且点P为△BMN内切圆上一点,求的最大值。已知函数的最大值为.(1)求常数的值;(2)求函数的单调递增区间;(3)若将的图象向左平移个单位,得到函数的图象,求函数在区间上的最大值和最小值.衡水万卷周测(十五)答案解析一、选择题DBC试题分析:由图象知:,因为,所以,解得:,所以这段时间水深的最大值是,故选C.考点:三角函数的图象与性质.ADBBDBDAD二、填空题2试题分析:因为=4=2(1+cosx)sinx-2sinx-=sin2x-所以函数的零点个数为函数y=sin2x与y=图像的交点的个数,函数y=sin2x与y=图像如图,由图知,两函数图像右2个交点,所以函数由2个零点。考点:1.二倍角的正弦、余弦公式,2.诱导公式,3.函数的零点.【答案】解析:根据二倍角公式,可将已知式子化简为:,由韦达定理可得:,根据同角三角函数基本关系式可得:,即,解得,又因为,所以,所以,故答案为.【思路点拨】由韦达定理以及同角三角函数基本关系式可求得,再根据,确定值,利用二倍角公式将已知式子降角升幂化简为,即可求得.【答案】三、解答题【答案】(Ⅰ)(II)【解析】(Ⅰ)已知等式(a+b)(sinA-sinB)=(c-b)sinC,利用正弦定理化简得:(a+b)(a-b)=c(c-b),即,∴cosA==,则A=;(Ⅱ)方程,解得:,,由cosB≤1,得到cosB=,∴sinB==,则sinC=sin(A+B)=×+×=.【思路点拨】(Ⅰ)已知等式利用正弦定理化简,整理得到关系式,再利...