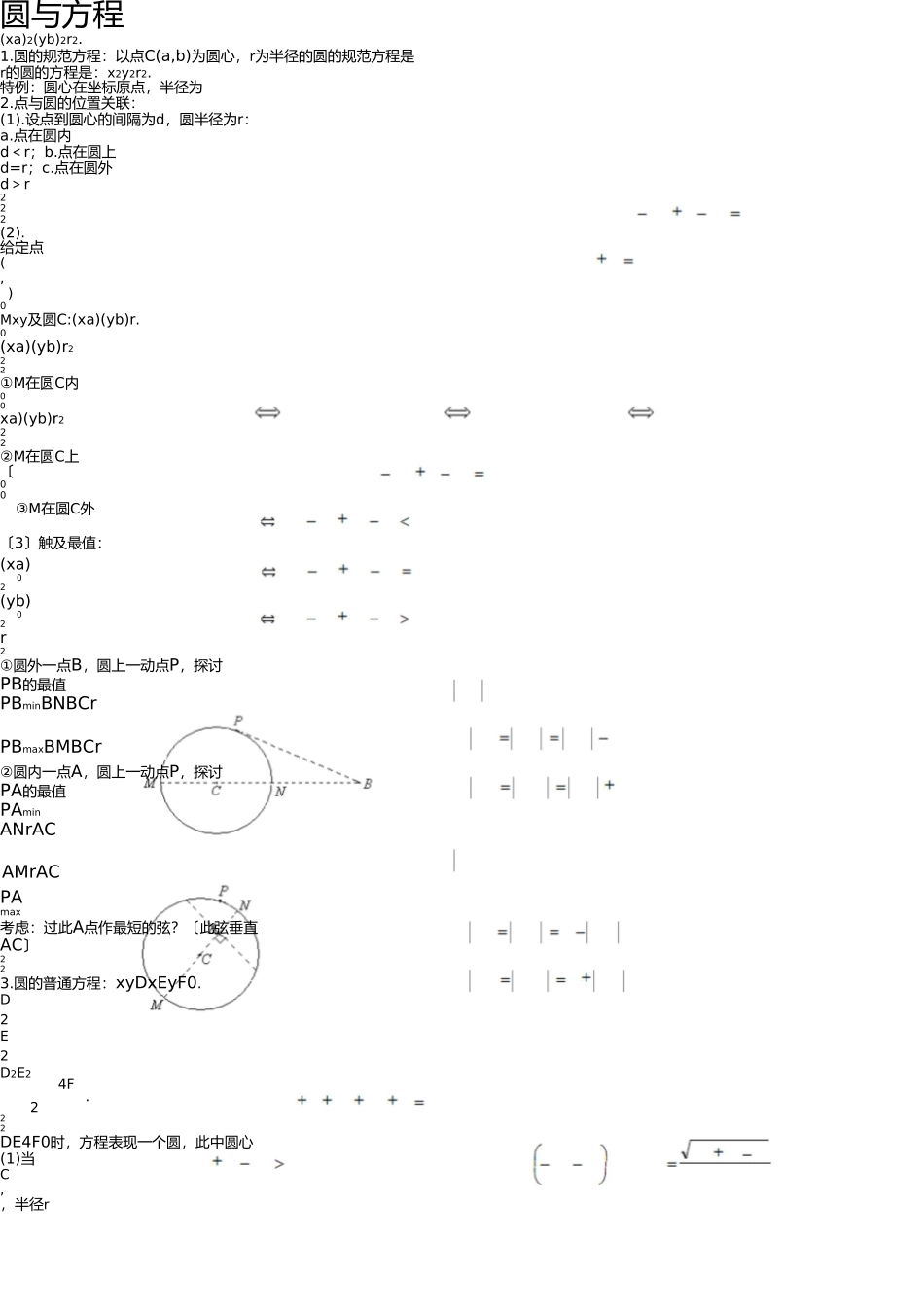
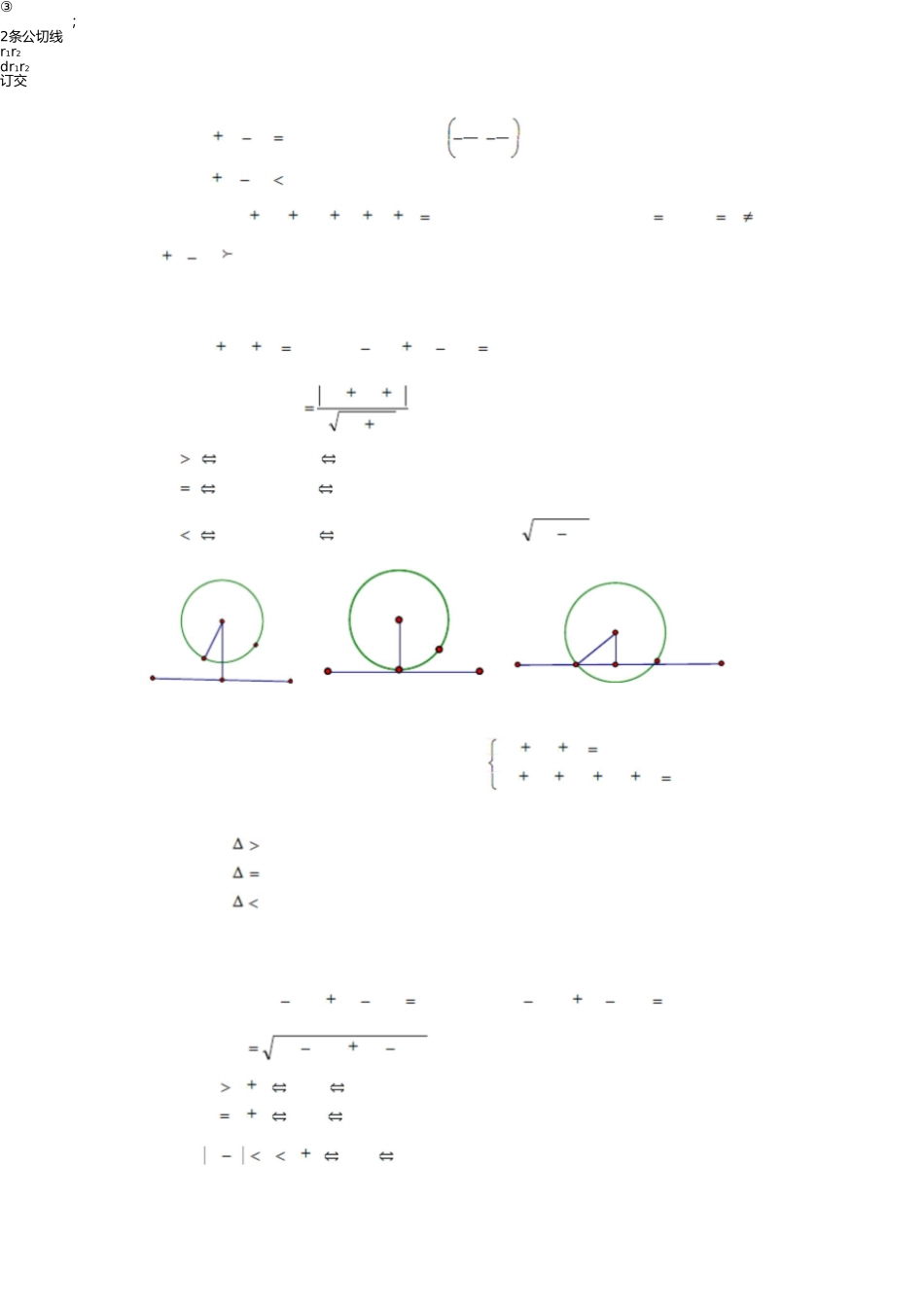
圆与方程(xa)2(yb)2r2.1.圆的规范方程:以点C(a,b)为圆心,r为半径的圆的规范方程是r的圆的方程是:x2y2r2.特例:圆心在坐标原点,半径为2.点与圆的位置关联:(1).设点到圆心的间隔为d,圆半径为r:a.点在圆内d<r;b.点在圆上d=r;c.点在圆外d>r222(2).给定点(,)0Mxy及圆C:(xa)(yb)r.0(xa)(yb)r222①M在圆C内00xa)(yb)r222②M在圆C上〔00③M在圆C外〔3〕触及最值:(xa)02(yb)02r2①圆外一点B,圆上一动点P,探讨PB的最值PBminBNBCrPBmaxBMBCr②圆内一点A,圆上一动点P,探讨PA的最值PAminANrACAMrACPAmax考虑:过此A点作最短的弦?〔此弦垂直AC〕223.圆的普通方程:xyDxEyF0.D2E2D2E24F.222DE4F0时,方程表现一个圆,此中圆心(1)当C,,半径rD2E2(2)当D2E24F0时,方程表现一个点.,22(3)当DE4F0时,方程不表现任何图形.注:方程Ax2BxyCy2DxEyF0表现圆的充要前提是:B0且AC0且D2E24AF0.4.直线与圆的位置关联:直线AxByC0与圆(xa)2(yb)2r2AaBbC圆心到直线的间隔dA2B21〕dr2〕dr无交点;直线与圆相离直线与圆相切只要一个交点;3〕dr;弦长|AB|=2rd22直线与圆订交有两个交点rd=rrddAxByC0还能够运用直线方程与圆的方程联破方程组的个数来揣摸:求解,经过解2x2yDxEyF0〔1〕当〔2〕当〔3〕当0时,直线与圆有2个交点,,直线与圆订交;0时,直线与圆只要1个交点,直线与圆相切;0时,直线与圆不交点,直线与圆相离;5.两圆的位置关联22,2222C:(xa)(yb)r2222〔1〕设两圆C:(xa)(yb)r与圆1111圆心距d(aa)(bb)221212①drr2外离外切4条公切线;1②drr213条公切线;③;2条公切线r1r2dr1r2订交④⑤1条公切线;dr1r2内切;0dr1r2内含无公切线外离外切订交内切〔2〕两圆大年夜众弦地点直线方程22圆CxyDxEyF0,:111122圆CxyDxEyF0,:2222DDxEEyFF20为两订交圆大年夜众弦方程那么.12121弥补阐明:①假设CC相切,那么表现此中一条公切线方程;与12②假设CC相离,那么表现连心线的中垂线方程与.12〔3〕圆系咨询题2222过两圆CxyDxEyF0CxyDxEyF0交点的圆系:跟:111122222222方程为xyDxEyF1xyDxEyF20〔1〕1122弥补:①上述圆系不包含C2;②2〕当1时,表现过两圆交点的直线方程〔大年夜众弦〕22③过直线AxByC0与圆xyDxEyF0交点的圆系方程为2x2yDxEyFAxByC06.过一点作圆的切线的方程:(1)过圆外一点的切线:①k不存在,验证能否成破②k存在,设点歪式方程,用圆心到该直线间隔=半径,即yy0k(xx)110byk(ax1)1R2R1求解k,失落失落落切线方程【确信两解】例1.经过点P(1—,2)点作圆(x+1)+(y—2)=4的切线,那么切线方程为22。x—a+y—b=r222x0,y0),,圆上一点为((2)过圆上一点的切线方程:圆()()那么过此点的切线方程为(x—a)(x—a)+(y—b)(y—b)=r200特不地,过圆xyr222P(x,y)2xxyyr.00上一点的切线方程为0022x++y+=例2.经过点P(—4—,8)点作圆(7)(8)9的切线,那么切线方程为。7.切点弦(1)过⊙C:(xa)(yb)r222P(x,y)作⊙C的两条切线,切点分不为A、B,00外一点那么切点弦AB地点直线方程为:(xa)(xa)(yb)(yb)r2008.切线长:a)2(y22b)=r,那么过圆外一点P(x,y)的切线长为00假设圆的方程为(x2(x0a)+(y0b)2r2d=.9.圆心的三个要紧多少多何性子:①圆心在过切点且与切线垂直的直线上;②圆心在某一条弦的中垂线上;③两圆内切或外切时,切点与两圆圆心三点共线。10.两个圆订交的大年夜众弦长及大年夜众弦地点的直线方程的求法2222例.已经清晰圆C:x+y—2x=0跟圆C:x+y+4y=0,试揣摸圆跟位置关联,12假设订交,那么设其交点为A、B,试求出它们的大年夜众弦AB的方程及大年夜众弦长。一、求圆的方程例1(06重庆卷文)以点(2,1)为圆心且与直线3x4y50相切的圆的方程为()2222(x2)(y1)3(x2)(y1)3(A)(B)2(x2)(y1)222(x2)(y1)99(C)(D)二、位置关联咨询题22xy1与圆xy2ay0(a0)不大年夜众点,那么a的取值范例2(06安徽卷文)直线围是()(0,21)(21,21)(A)(C)(B)(21,21)(0,21)(D)三、切线咨询题22520相切的直线方程为()例3(06重庆卷理)过坐标原点且与圆xy4x2y11x3y3xy或xy3xy(B)或(A)311x3(C)y3x或yx(D)y3x或y3四、弦长咨询题22例4(06天津卷理)设直线axy30与圆、(x1)(y2)4订交于AB两点,且a弦AB的长为23,那么.五、夹角咨询题...