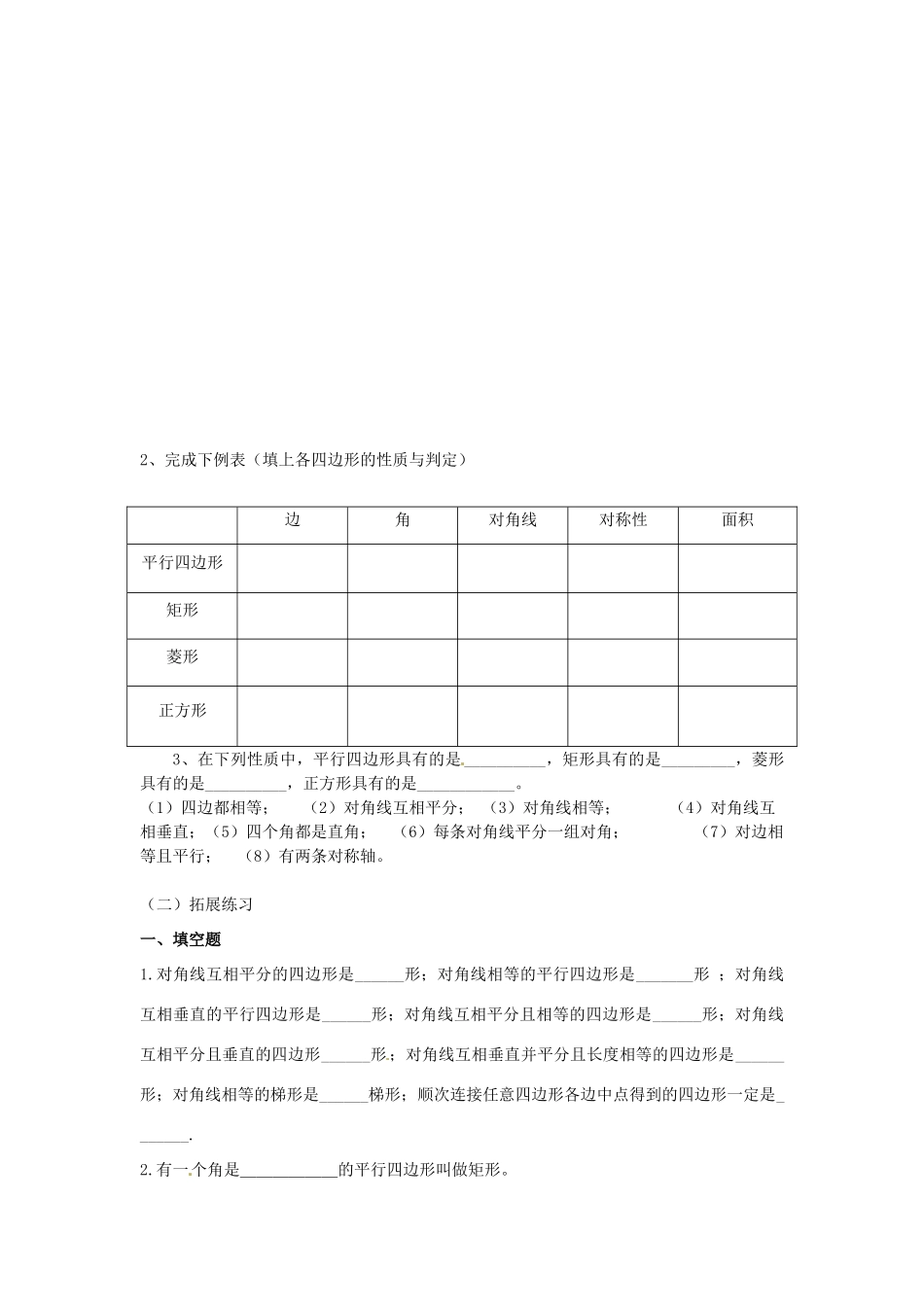
四边形复习重点、难点透视:1.重点:特殊四边形的性质与判定。2.难点:特殊四边形性质与判定的灵活应用。教学过程:一、引入:(教师提问)我们学习了哪些特殊的四边形?我们从哪些方面来研究这些四边形的性质?(学生回答)平行四边形,矩形、菱形、正方形;边、角、对角线、面积、对称性。(教师)这节课我们来复习平行四边形及特殊的平行四边形,首先请同学们独立完成手中的学案,然后在小组内交流讨论。学案:(一)复习巩固1、请完成下面的关系图一2、完成下例表(填上各四边形的性质与判定)边角对角线对称性面积平行四边形矩形菱形正方形3、在下列性质中,平行四边形具有的是__________,矩形具有的是_________,菱形具有的是__________,正方形具有的是____________。(1)四边都相等;(2)对角线互相平分;(3)对角线相等;(4)对角线互相垂直;(5)四个角都是直角;(6)每条对角线平分一组对角;(7)对边相等且平行;(8)有两条对称轴。(二)拓展练习一、填空题1.对角线互相平分的四边形是______形;对角线相等的平行四边形是_______形;对角线互相垂直的平行四边形是______形;对角线互相平分且相等的四边形是______形;对角线互相平分且垂直的四边形______形;对角线互相垂直并平分且长度相等的四边形是______形;对角线相等的梯形是______梯形;顺次连接任意四边形各边中点得到的四边形一定是_______.2.有一个角是______的平行四边形叫做矩形。3.如果要判定一个四边形是菱形,那么它的对角线应满足的条件是_________________。4.已知菱形的两条对角线的长分别是6和8,那么它的边长是_______。5.若菱形的周长为24cm,一个内角为60°,则菱形的面积为______。6.正方形的对角线的长与它的边长的比是______。7.对角线长为10cm的正方形的边长是______,面积是______。8.在ABCD中,∠A+∠C=270°,则∠B=______,∠C=______.。9.在ABCD中,两邻边的差为4cm,周长为32cm,则两邻边长分别为________.10.如果梯形的上底长为4cm,下底长为10cm,那么它的中位线长为________cm。11.等腰梯形的上底是10cm,下底是14cm,高是2cm,则等腰梯形的周长为______cm.12.如果梯形的面积为216cm2且两底长的比为4:5,高为16cm,那么两底长分别为________。13.如图1,平行四边形ABCD中,E,F分别为AD,BC边上的一点.若再增加一个条件_________,就可得BE=DF。14.将一矩形纸条,按如图2所示折叠,则∠1=_______度。15.如图3,矩形ABCD中,MN∥AD,PQ∥AB,则S1与S2的大小关系是______。图1图2图316.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB=_______.17.如图,在梯形ABCD中,AD∥BC,DE∥AB,△DEC的周长为10cm,BE=5cm,则该梯形的周长为。18.有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2a+b),宽为(a+b)的矩形,则需要A类卡片____张,B类卡片____张,C类卡片____张。__E_D_C_B_A19.如图,等腰梯形ABCD中,AD∥BC,∠B=45°,AE⊥BC于点E,AE=AD=2cm,则这个梯形的中位线长为_____cm.20.如图,l是四形形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD②AB=BC③AB⊥BC④AO=OC其中正确的结论是。(把你认为正确的结论的序号都填上)二、选择题21.能够判定一个四边形是平行四边形的条件是()A、一组对角相等B、两条对角线互相平分C、两条对角线互相垂直D、一对邻角的和为180°22.中,的值可以是()A.1:2:3:4B.1:2:2:1C.2:2:1:1D.2:1:2:123.用两块完全相同的直角三角形拼下列图形:①平行四边形②矩形③菱形④正方形⑤等腰三角形⑥等边三角形,一定能拼成的图形是()A、①④⑤B、②⑤⑥C、①②③D、①②⑤24.如图4,梯形ABCD中,对角线AC与BD交于点O,则图中面积相等的三角形有()。A.3对B.2对C.1对D.4对25.如图5,将矩形ABCD沿对角线BD对折,使点C落在C′处,BC′交AD于F,下列不成立的是()。A.AF=C′FB.BF=DFC.∠BDA=∠ADC′D.∠ABC′=∠ADC′26.如图6,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF.则∠CDF等于()。A.80°B.70°C.65°D.60°图4图...