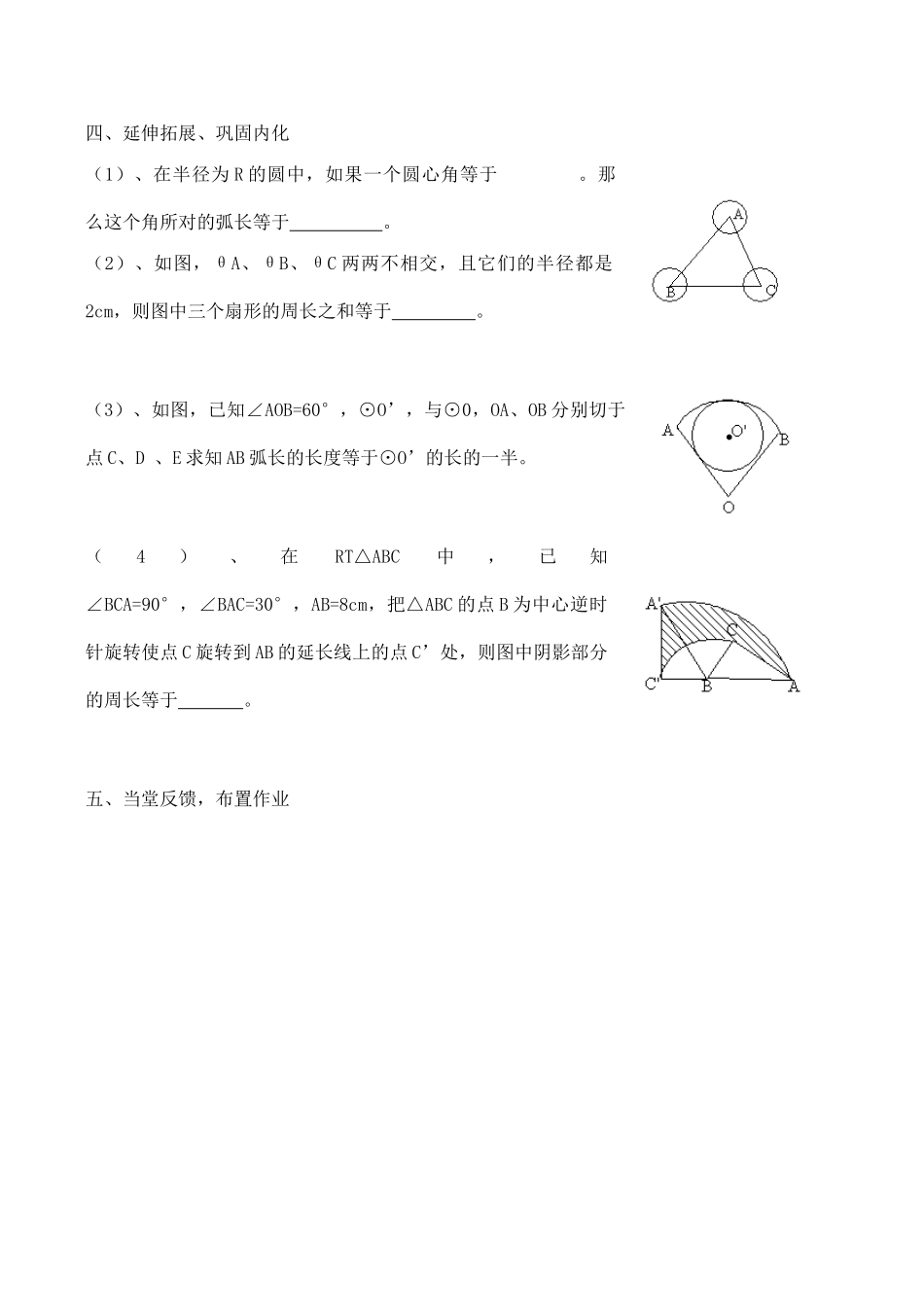
弧长和扇形面积第1课时[目标预设]一、知识与技能(1)以描述实际问题中的数量关系为背景,推导出弧长公式。(2)会运用弧长公式进行有关的计算。二、过程与方法(1)从具体到抽象,从特殊到一般,体会归纳思想。(2)能从具体情境中归纳出数量关系,经历对具体问题的探索过程。三、情感、态度、价值观:通过师生共同交流,探讨,使学生在掌握知识的基础上,认识事物的内在联系。[教学重点与难点]一、重点:弧长公式二、难点:利用弧长公式求实际问题中的有关计算[教学程序]一、创设情境、谈话导入:(1)圆周长公式:C=2πR,其中π是圆周率,R为圆的半径。(2)什么叫圆心角?圆心角为1°的所对弧长与该圆周长之间的关系怎样?(3)由课本的引例中,引出计算弧长的问题,要计算弧长,其实质计算n°的圆心角怕对弧长的问题,能否导出弧长的计算公式。计算弧长,必须知道圆的半径R或直径d及弧所对的圆心角n,则弧长公式和相信同学们能推导出。4、练习:课本P120引例弧长二、精讲点拔、质疑问难(1)、弧长公式:,在这个公式中,已知三个量l、n、R中的两个量,就可以求出第三个量。例:已知圆心角为120°,其所对弧长为6π求该圆的半径。例:有一条弧长为18π,圆的直径为12,求弧所对圆心角。例:已知圆周长为6π,圆周上一段弧所对的圆心角为80°,求该弧长。(2)、学生练习课本P122、1、三、课堂活动、强化训练(1)、如图,已知PA、PB切θO于A、B两点、OP=4cm,∠APB=60°,求阴影部分的周长。(2)、一块边长为a的正方形木板ABCD在水平的桌面上绕点D顺时针方向旋转即A’B’C’D’的位置,顶点B从开始到结束时所经过的路径长。四、延伸拓展、巩固内化(1)、在半径为R的圆中,如果一个圆心角等于。那么这个角所对的弧长等于。(2)、如图,θA、θB、θC两两不相交,且它们的半径都是2cm,则图中三个扇形的周长之和等于。(3)、如图,已知∠AOB=60°,⊙O’,与⊙0,OA、OB分别切于点C、D、E求知AB弧长的长度等于⊙O’的长的一半。(4)、在RT△ABC中,已知∠BCA=90°,∠BAC=30°,AB=8cm,把△ABC的点B为中心逆时针旋转使点C旋转到AB的延长线上的点C’处,则图中阴影部分的周长等于。五、当堂反馈,布置作业