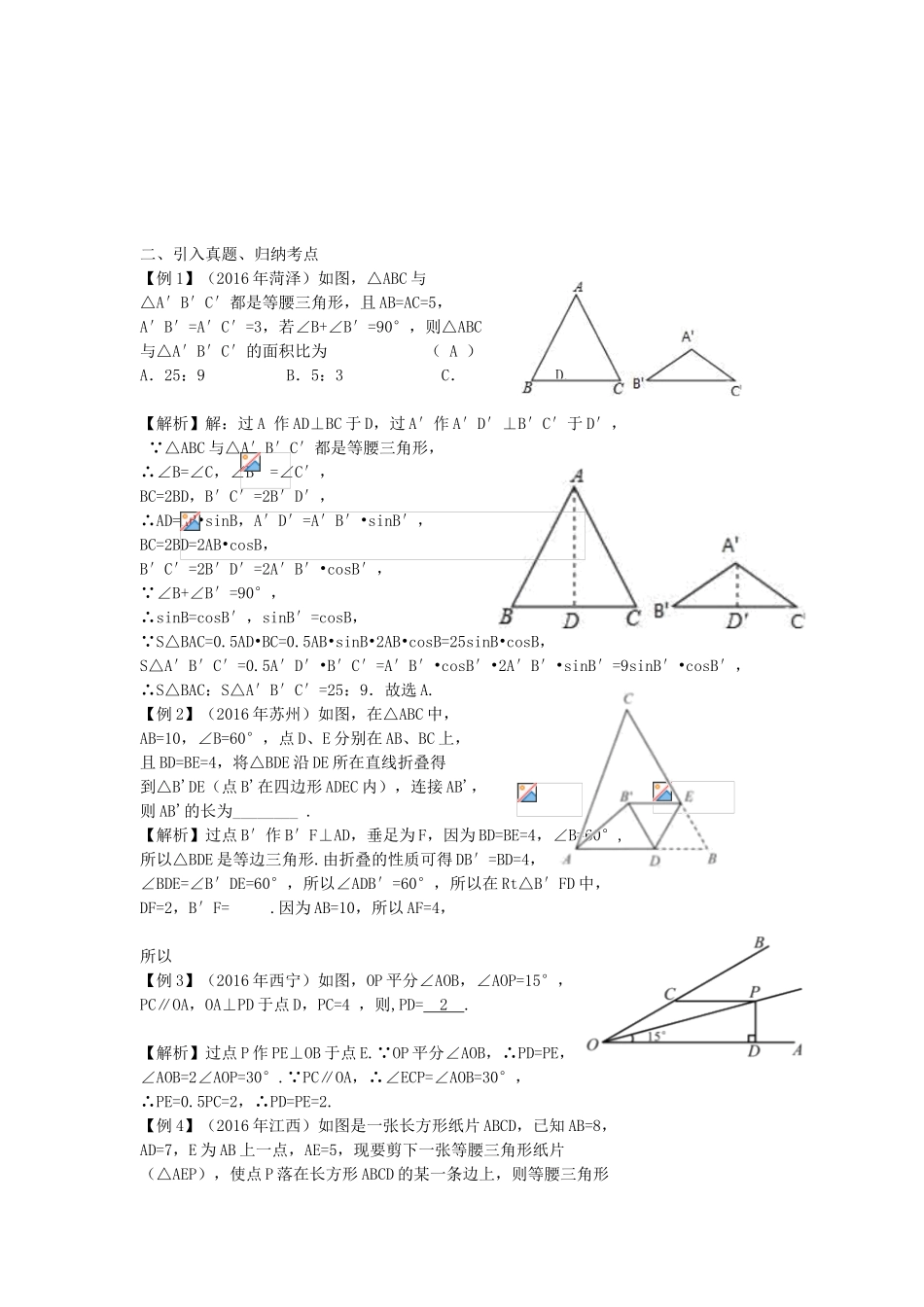
第五单元三角形第21课时等腰三角形及直角三角形教学目标【考试目标】1.了解等腰三角形的有关概念,掌握等腰三角形的性质和一个.三角形为等腰三角形的条件;了解等边三角形的概念及性质;2.了解直角三角形的概念,掌握直角三角形的性质和一个三角形是直角三角形的条件;3.会运用勾股定理解决简单问题;会用勾股定理的逆定理判定一个三角形是否为直角三角形.【教学重点】1.了解掌握等腰三角形的有关概念及性质.2.学会等腰三角形的判定.3.掌握等边三角形的性质及判定方法.4.掌握线段垂直平分线与角平分线的相关性质.5.学会直角三角形的相关性质与判定方法.教学过程一、体系图引入,引发思考二、引入真题、归纳考点【例1】(2016年菏泽)如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为(A)A.25:9B.5:3C.D.【解析】解:过A作AD⊥BC于D,过A′作A′D′⊥B′C′于D′,∵△ABC与△A′B′C′都是等腰三角形,∴∠B=∠C,∠B′=∠C′,BC=2BD,B′C′=2B′D′,∴AD=AB•sinB,A′D′=A′B′•sinB′,BC=2BD=2AB•cosB,B′C′=2B′D′=2A′B′•cosB′,∵∠B+∠B′=90°,∴sinB=cosB′,sinB′=cosB,∵S△BAC=0.5AD•BC=0.5AB•sinB•2AB•cosB=25sinB•cosB,S△A′B′C′=0.5A′D′•B′C′=A′B′•cosB′•2A′B′•sinB′=9sinB′•cosB′,∴S△BAC:S△A′B′C′=25:9.故选A.【例2】(2016年苏州)如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B'DE(点B'在四边形ADEC内),连接AB',则AB'的长为________.【解析】过点B′作B′F⊥AD,垂足为F,因为BD=BE=4,∠B=60°,所以△BDE是等边三角形.由折叠的性质可得DB′=BD=4,∠BDE=∠B′DE=60°,所以∠ADB′=60°,所以在Rt△B′FD中,DF=2,B′F=.因为AB=10,所以AF=4,所以【例3】(2016年西宁)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,OA⊥PD于点D,PC=4,则,PD=2.【解析】过点P作PE⊥OB于点E.∵OP平分∠AOB,∴PD=PE,∠AOB=2∠AOP=30°.∵PC∥OA,∴∠ECP=∠AOB=30°,∴PE=0.5PC=2,∴PD=PE=2.【例4】(2016年江西)如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是.【解析】据题意,如果点P落在AD边上,则AE=AP=5,底边长PE2=AP2+AE2=52+52=50,PE=;如果点P落在DC边上,则底边长AE=5;如果点P落在BC边上,则两条腰AE=EP=5,所以所以等腰三角形AEP的底边长是或5或.三、师生互动,总结知识先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.课后作业布置作业:同步导练教学反思学生对特殊三角形的掌握情况很好,望多加复习巩固,做到熟练会用.