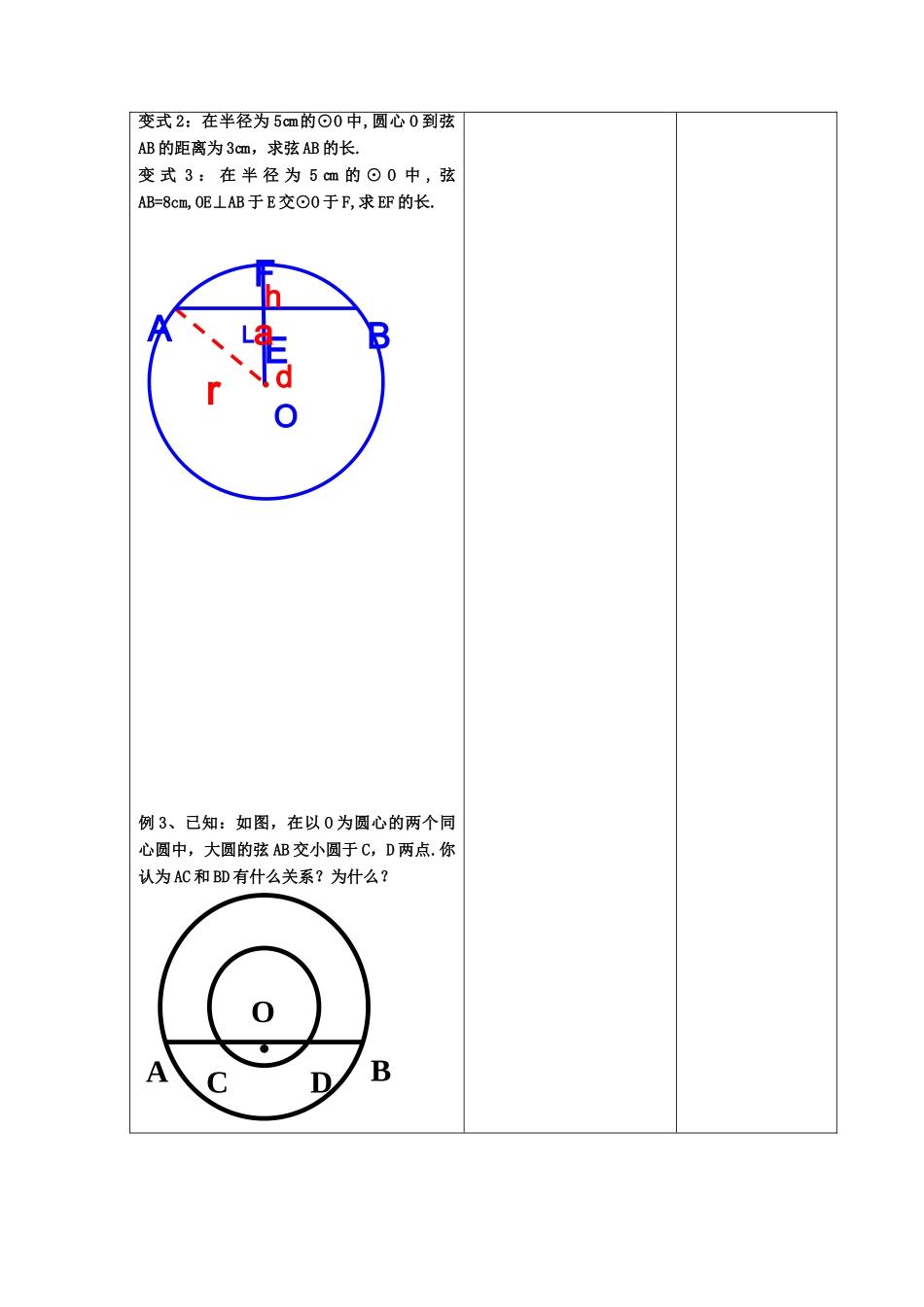
教学课题5.2圆的对称性(二)课型新授教学目标:1.理解圆的对称性(轴对称)及有关性质.2.理解垂径定理并运用其解决有关问题.教学重点:垂径定理及其运用.教学难点:灵活运用垂径定理.教学方法与手段:多媒体教学过程:教师活动学生活动设计意图一、情境创设(1)什么是轴对称图形?(2)如何验证一个图形是轴对称图形?复习引入二、探究学习1.尝试(1)在圆形纸片上任意画一条直径.(2)沿直径将圆形纸片对折,你能发现什么?请将你的发现写下来:____________________.动手操作探究垂径定理2.探索如图,CD是⊙O的弦,画直径AB⊥CD,垂足为P;将圆形纸片沿AB对折通过折叠活动,你发现了什么?3.总结垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。三.典型例题例1:在半径为5㎝的⊙O中,弦AB=8㎝,求点O与弦AB的距离.变式1、如图,已知在⊙O中,弦AB的长为8㎝,圆心O到AB的距离为3㎝,求⊙O的半径.变式2:在半径为5㎝的⊙O中,圆心O到弦AB的距离为3㎝,求弦AB的长.变式3:在半径为5㎝的⊙O中,弦AB=8cm,OE⊥AB于E交⊙O于F,求EF的长.例2:在半径为5㎝的⊙O中,弦AB=8㎝,求点O与弦AB的距离.变式1、如图,已知在⊙O中,弦AB=8㎝,圆心O到AB的距离为3㎝,求⊙O的半径.垂径定理并运用其解决有关问题EOAB54变式2:在半径为5㎝的⊙O中,圆心O到弦AB的距离为3㎝,求弦AB的长.变式3:在半径为5㎝的⊙O中,弦AB=8cm,OE⊥AB于E交⊙O于F,求EF的长.例3、已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.你认为AC和BD有什么关系?为什么?EOAB└Frhda.ACDBO巩固练习1、在⊙O中,弦CD=8cm,圆的直径是10cm,则圆心O到弦CD的距离是____cm2、在⊙O中弦CD=24,圆心O到弦CD的距离为5,则⊙O的直径是_______3、若AB为⊙O的直径,弦CD⊥AB于E,AE=16,BE=4,则CD=_______如图,AB、CD是⊙O的两条平行弦,AC与BD相等吗?为什么?加深对垂径定理的理解•o•oCCDDEE••CCDDOOEE••AABBDDCCEEOO拓展与延伸1、如图,⊙O的直径为10,弦AB的长为8,P是弦AB上的动点.①线段OP的长的最小值为___,最大值为___.②OP的取值范围是___________;③使线段OP的长度为整数值的P点位置有个.2.如图,CD为⊙O的直径,弦AB交CD于E,∠CEB=30°,DE=9㎝,CE=3㎝,求弦AB的长会用垂径定理并运用其解决有关问题●OABCD三、归纳总结圆的轴对称性及有关性质.巩固本节知识点,检测教学效果四、作业:同步练习76-77授后小记:在学生经历探索和证明垂径定理的过程中,进一步体会和理解研究几何图形的各种方法授课日期10月30日EDOCABF└