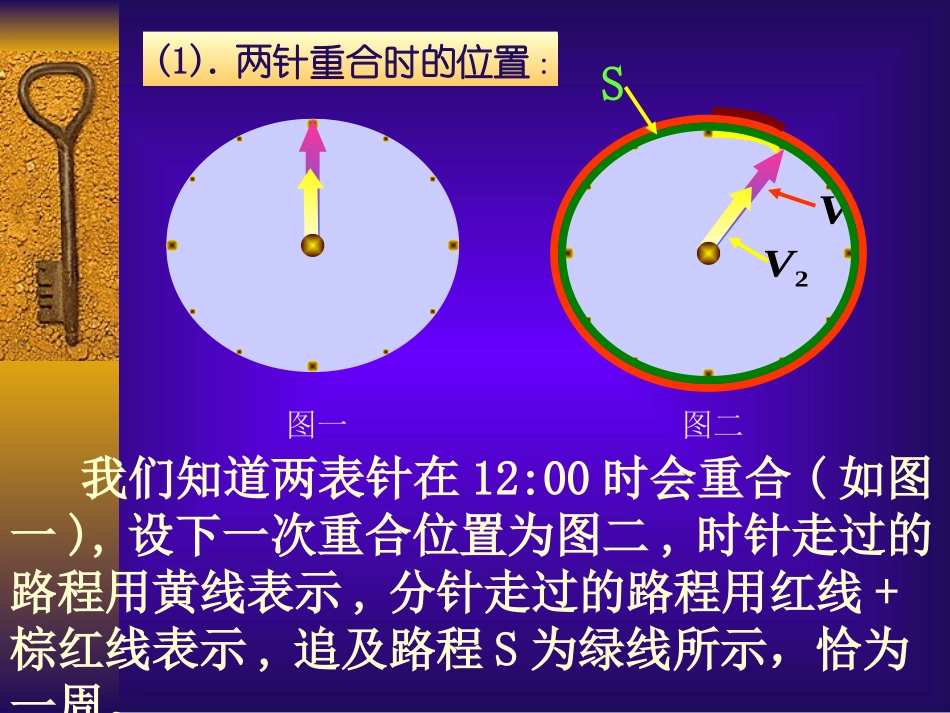
同学们,我们每天的日常生活都离不开表,但是你们知道表中还隐藏着什么样的有趣的数学知识吗?让我们一起研究研究。不知你是否观察过钟表上的时针和分针,它们总是成一定角度。那么,你是否知道它们什么时候重合?什么时候成一条直线?什么时候成直角?其中有什么规律?问题一:这类问题实际上是分针追时针的追击问题,它的公式是:21VVST追(1).两针重合时的位置:图一图二我们知道两表针在12:00时会重合(如图一),设下一次重合位置为图二,时针走过的路程用黄线表示,分针走过的路程用红线+棕红线表示,追及路程S为绿线所示,恰为一周。1V2VS解法一:取钟表上的一小格(即一分钟)为单位路程,则)(60格S)/(11分格V)/(1212分格V(分)追1156511720121160T解法二:取钟表上的一大格(即一小时)为单位路程,则)(12格S)/(121时格V)/(12时格V(分)(时)追115656011111111111211212T结果相同。根据以上计算,每隔分时针和分针重合一次。11565在一天中它们重合的次数是:(次)22117206024N它们的位置分别是:00:24,11654:22,11149:21,11743:20,11238:19,11832:18,11327:17,11921:16,11416:15,111010:14,1155:13,00:12,11654:10,11149:9,11743:8,11238:7,11832:6,11327:5,11921:4,11416:3,111010:2,1155:1(2).两针成一线时的位置:图一我们知道两表针在6:00时会成与一线(如图一),设下一次成一线的位置为图二,时针走过的路程用黄线表示,分针走过的路程用红线+棕红线表示,追及路程S为绿线所示,恰好为一周,因此,此问题的解答与(1)完全类似。即每隔分时针和分针成一线,一天内表针将22次成一线。11565图二S1V2V(3).两针垂直时的位置:两表针在3:00时垂直(如图一),设下一次垂直的位置为图二,时针走过的路程用黄线表示,分针走过的路程用红线表示,追及路程S为绿线所示。由于蓝角与绿角互补,红角也与绿角互补,所以,红角=蓝角,故图中两黄线部分相等。因此,追及路程恰好为半周。图一图二2V1VS解:取钟表上的一小格(即一分钟)为单位路程,则)(30格S)/(11分格V)/(1212分格V(分)追1183211360121130T方法二:S图一图二将时针看作是不动的,分针以相对时针的速度(二者的速度差)追及时针。两表针在3:00时垂直(如图一),下一次垂直的位置为图二,分针走过的路程用绿线表示,这也就是追及的路程S,恰好为圆周的半圈。时分VV解:取钟表上的一小格(即一分钟)为单位路程,则)(30格S)/(12111分格V)/(02分格V(分)追1183211360012130T当两针再次重合时,又回到图一的情况,因此,每隔分两针相互垂直11832根据以上计算,每隔分时针和分针垂直一次。11832在一天中它们重合的次数为(次)44113606024N它们的位置分别是:.11327:2,,00:9,11327:8,11654:7,11921:7,11149:6,11416:6,11743:5,111010:5,11238:4,1155:4,11832:3,00:3时针与分针还可以成20度、30度或其它度数的角,它们在一天中会出现几次?分别在哪些位置?其实,分析方法与相互垂直时完全类似,请你也试一试。推广:在分析此问题时,我们用到了追及问题的知识、数形结合法、用字母表示数、求代数式的值以及圆和角度的一些知识。小结:问题二:如果一个工人师傅错把一块表的时针和分针安反了,那么这块表还能正确表示所有时间吗?答案是否定的,除了两针重合时能正确表示时间外,表针在其它位置均无法表示时间例如:正常装错3:0012:00?×12:15?×问题三:表是用来反映时间的工具,但如果你的表不准,你是否可以根据它来判断其他人的表准不准呢?答案是肯定的。下面由我来告诉你们方法。设:表A比标准时间一小时快a,表B比表A每小时快b。那么,表B是否准确?分析:标准时间一小时中B所走的时间:当A走1小时时,B走b+1小时;当标准时为1小时时,A走a+1小时;设:B走x小时。A、B两表速度成比例,应有:111bax)1)(1(bax准若Bba1)1)(1(不准若Bba1)1)(1(这就是判断B表准不准的判据。下面,让我们根据上面的判据来判断一下:分析:)(601)(601时时ba不准)(13600359960596061]6011)[6011()1)(1(ba例:我的表比标准时间每小时快1分,王骁的表比我的表每小时慢1分,王骁的表准吗?分析此问题时,我们应用了比例的性质、用字母表示数、用负数表示相反意义的量、列代数式、化简代数式及有理数运算六大知识。小结: