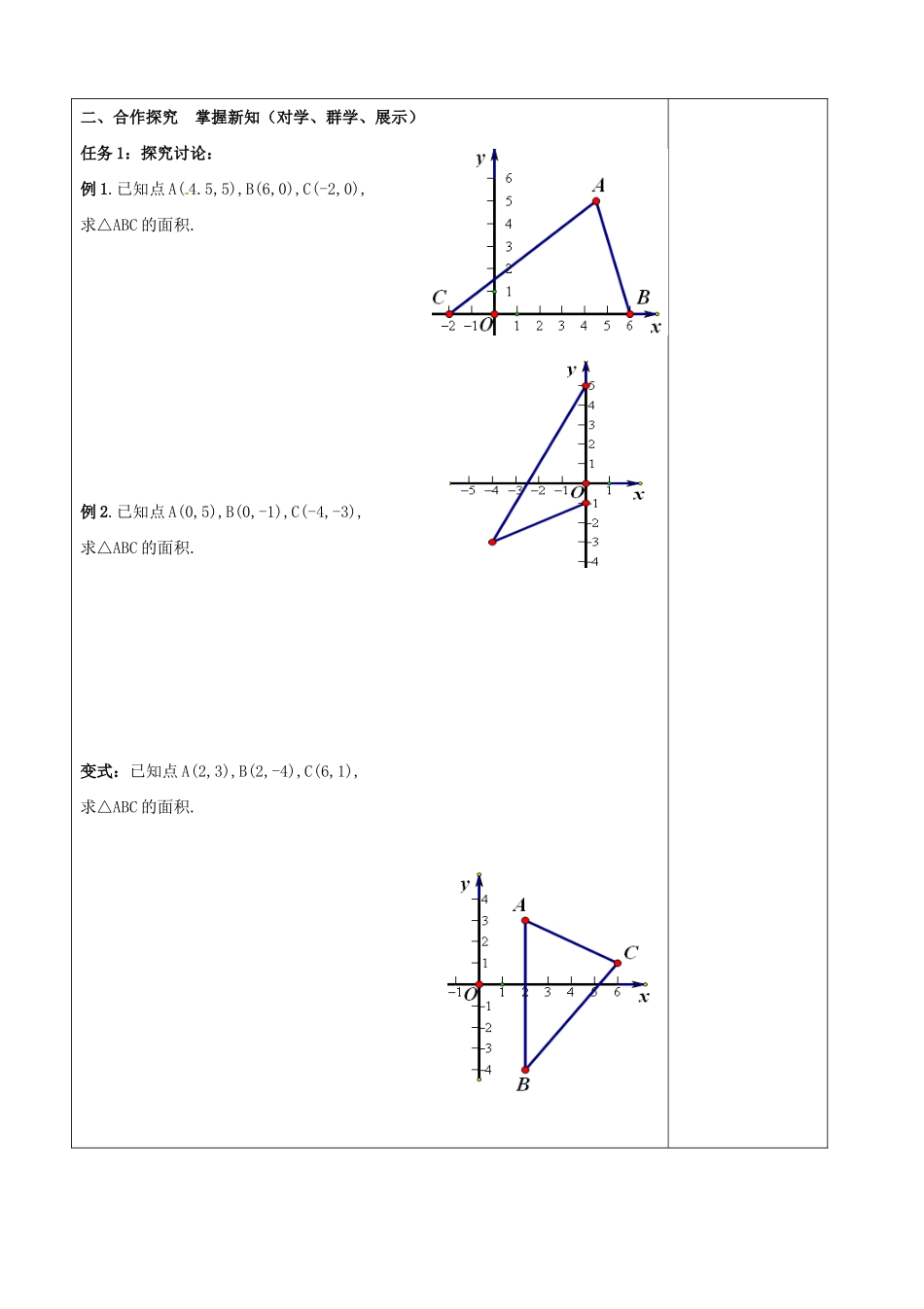
7.2《坐标方法的简单应用》学习目标1.掌握坐标系中求解图形面积这一类型问题的方法.2、转化、数形结合、方程以及分类讨论的思想的综合应用学习重点掌握坐标系中求解图形面积这一类型问题的方法.学习难点转化、数形结合、方程以及分类讨论的思想的综合应用学习过程教师二次备课与学生笔记一、自主学习了解新知(独学)任务1:复习旧知:1、三角形面积公式:S=平行四边形面积公式:S=梯形面积公式:S=2、作出下列图形的高3、坐标系中点的坐标特点P(x,y)横坐标为,纵坐标为,到x轴的距离为,到y轴的距离为P(x,y)在x轴上,则;P(x,y)在y轴上,则;二、合作探究掌握新知(对学、群学、展示)任务1:探究讨论:例1.已知点A(4.5,5),B(6,0),C(-2,0),求△ABC的面积.例2.已知点A(0,5),B(0,-1),C(-4,-3),求△ABC的面积.变式:已知点A(2,3),B(2,-4),C(6,1),求△ABC的面积.三、拓展提高巩固新知(小组合作,学能展示)1、已知点A(-2,1),B(1,-3),C(3,4),求△ABC的面积.如图A(-4,0),B(6,0),C(2,4),D(-3,2).(1)求四边形ABCD的面积;(2)在y轴上找一点P,使△APB的面积等于四边形的一半.求P点坐标.四、发现总结提升知识教学反思我学到的知识我学到的方法与思想我的疑惑