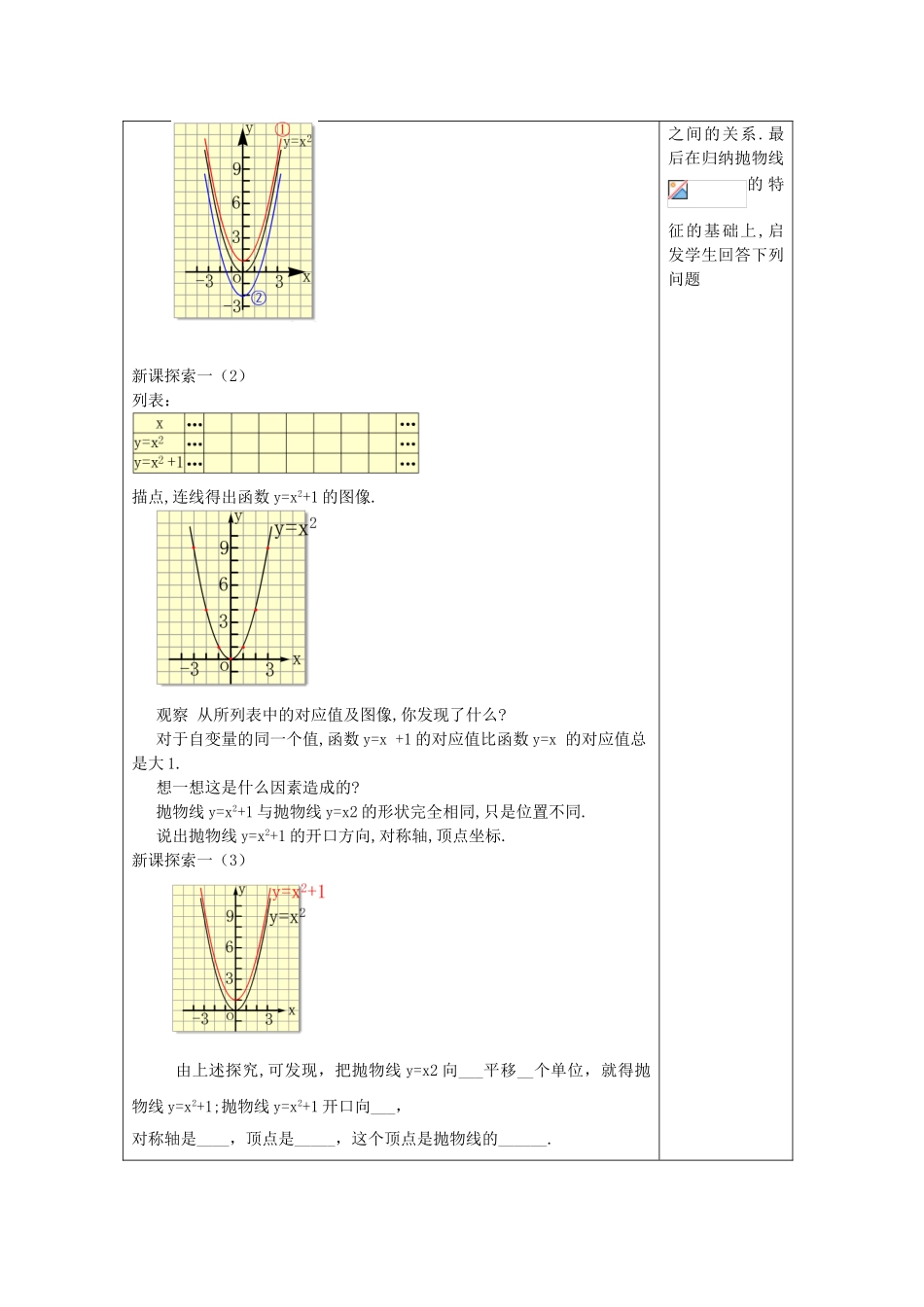
二次函数y=ax2+c的图像课题26.2(2)二次函数y=ax2+c的图像课型新授课教学目标能画出二次函数的图像理解抛物线y=ax2+c图像的特点,理解与y=ax2的区别与联系重点理解抛物线y=ax2+c图像的特点难点理解抛物线y=ax2+c图像的特点教学准备学生活动形式教学过程设计意图课题引入:课前练习一1,填空:(1)二次函数y=--x2的图像是_______,它的开口______,对称轴是______,顶点是_____,顶点是抛物线的最___点;(2)二次函数y=3x2的图像是_______,它的开口______,对称轴是______,顶点是_____,顶点是抛物线的最___点.课前练习二2.已知顶点为原点,对称轴为y轴的抛物线经过点(-3,-6),求表示这条抛物线的解析式.解:根据题意,设所求的抛物线的解析式为y=ax2.由抛物线经过点(-3,-6),得9a=-6.解得a=--.∴所求的函数解析式是y=--x2.课前一,二是对上一课时所学知识的强化练习新探一研究二次函数的图像及特征.课件首先从解析式上着手,让学生观察函数的异同,一开始就抓住关键要素,以利于后面的进一步探索.接着让学生猜想,然后环绕着这个猜想,用描点法加以验证.从而得出函数的图像也是抛物线,并获得两条抛物线知识呈现:新课探索一(1)观察试比较函数y=x2+1与y=x2的异同.猜想函数y=x2+1的图像与抛物线y=x2之间有什么关系?你认为图中哪条曲线是函数y=x2+1的图像?新课探索一(2)列表:描点,连线得出函数y=x2+1的图像.观察从所列表中的对应值及图像,你发现了什么?对于自变量的同一个值,函数y=x+1的对应值比函数y=x的对应值总是大1.想一想这是什么因素造成的?抛物线y=x2+1与抛物线y=x2的形状完全相同,只是位置不同.说出抛物线y=x2+1的开口方向,对称轴,顶点坐标.新课探索一(3)由上述探究,可发现,把抛物线y=x2向___平移__个单位,就得抛物线y=x2+1;抛物线y=x2+1开口向___,对称轴是____,顶点是_____,这个顶点是抛物线的______.之间的关系.最后在归纳抛物线的特征的基础上,启发学生回答下列问题思考由上述探究的启示,请说一说:将抛物线y=x2向___平移__个单位,可得抛物线y=x2-1.抛物线y=x2-1开口向___,对称轴是____,顶点是______,这个顶点是抛物线的_______.新课探索二想一想,议一议函数y=-x2-2,y=-x2+2的图像与函数y=-x2图像之间有怎样的关系?二次函数y=-x2-2的图像,是一条_______,这条抛物线的开口____;它的对称轴是____;顶点是______,这个顶点是抛物线的_______;二次函数y=-x2+2的图像,是一条_____,这条抛物线的开口____;它的对称轴是____;顶点是_____,这个顶点是抛物线的_______.新课探索三一般地,二次函数y=ax2+c(其中a,c是常数,且a≠0)的图像是抛物线,称为抛物线y=ax2+c,它可通过将抛物线y=ax2向上(c>0时)或向下(c<0时)平移|c|个单位得到.抛物线y=ax2+c(其中a,c是常数,且a≠0)的对称轴是y轴,即直线x=0;顶点坐标是(0,c).抛物线的开口方向由a所取值的符号决定,当a>0时,它的开口向上,顶点是抛物线的最低点;当a<0时,它的开口向下,顶点是抛物线的最高点.课内练习一1.(1)将抛物线y=x2向___平移___个单位,可得抛物线y=x2+1,这条抛物线的开口_____,对称轴是_______,顶点坐标是______;(2)将抛物线y=-x2向___平移___个单位,可得抛物线y=-x2-1,这条抛物线的开口____,对称轴是_____,顶点坐标是____.课内练习二2.(1)将抛物线y=2x2向下平移5个单位,所得到的抛物线的表达式为________;(2)试一试将抛物线y=-2x2-3向___平移___个单位,可得抛物线y=-2x2+1.课堂小结:二次函数y=ax2+c的图像1.一般地,二次函数y=ax2+c(其中a,c是常数,且a≠0)的图像是抛物线,称为抛物线y=ax2+c,它可通过将抛物线y=ax2向上(c>0时)或向下(c<0时)平移|c|个单位得到.2.抛物线y=ax2+c的特征抛物线y=ax2+c(其中a,c是常数,且a≠0)的对称轴是y轴,即直线x=0;顶点坐标是(0,c).抛物线的开口方向由a所取值的符号决定,当a>0时,它的开口向上,顶点是抛物线的最低点;当a<0时,它的开口向下,顶点是抛物线的最高点.课外作业练习册预习要求预习二次函数y=a(x+m)2图像性质教学后记与反思1、课堂时间消耗:教师活动15分钟;学生活动25分钟)2、本课时实际教学效果自评(满分10分):分3、本课成功与不足及其改进措施: