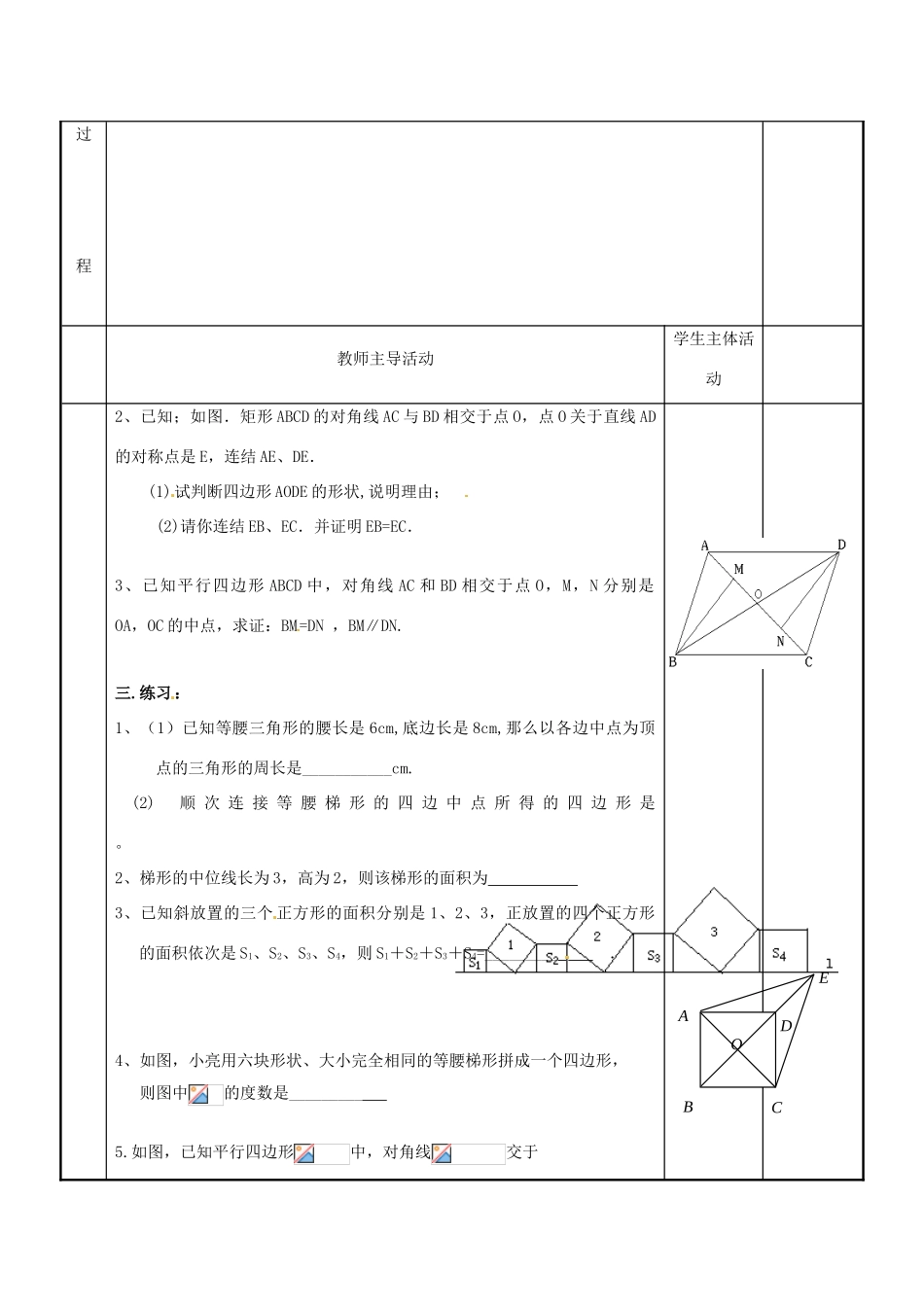
小结与思考(2)课题课型新授课教学目标通过对本章知识的小结与梳理,进一步掌握等腰三角形的性质和判定、直角三角形全等的判定、角平分线的性质定理与判定定理、特殊四边形(平行四边形、矩形、菱形、正方形)的定义、性质和判定;等腰梯形的性质和判定;中位线定理,并会灵活运用.重点复习本章所学知识点难点复习本章所学知识点教法及教具讲练结合三角板教学过程教学内容个案调整教师主导活动学生主体活动一、基础练习1、等腰三角形的一个底角为,则顶角的度数是度.2、等腰三角形的两边长分别为4和9,则第三边长为.3、下列命题为真命题的是()A:三角形的中位线把三角形的面积分成相等的两部分;B:对角线相等且相互平分的四边形是正方形;C:关于某直线对称的两个三角形是全等三角形;D:一组对边平行,另一组对边相等的四边形一定是等腰梯形4、下列命题是假命题的是()A:四个角相等的四边形是矩形;B:对角线互相平分的四边形是平行四边形;C:四条边相等的四边形是菱形;D:对角线互相垂直且相等的四边形是正方形5、在中,∠ABC的平分线交AD于E,且AE=2,DE=1,则的周长等于.6、如图,点D、E、F分别是三边上的中点.若的面积为12,则的面积为.二、例题学习1、如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.(1)求证:AD⊥CF;(2)连接AF,试判断△ACF的形状,并说明理由.教学教学内容个案调整(第5题)过程教师主导活动学生主体活动2、已知;如图.矩形ABCD的对角线AC与BD相交于点O,点O关于直线AD的对称点是E,连结AE、DE.(1)试判断四边形AODE的形状,说明理由;(2)请你连结EB、EC.并证明EB=EC.3、已知平行四边形ABCD中,对角线AC和BD相交于点O,M,N分别是OA,OC的中点,求证:BM=DN,BM∥DN.三.练习:1、(1)已知等腰三角形的腰长是6cm,底边长是8cm,那么以各边中点为顶点的三角形的周长是___________cm.(2)顺次连接等腰梯形的四边中点所得的四边形是。2、梯形的中位线长为3,高为2,则该梯形的面积为3、已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________.4、如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中的度数是_________5.如图,已知平行四边形中,对角线交于ECDBAO点,是延长线上的点,且是等边三角形.(1)求证:四边形是菱形;(2)若,求证:四边形是正方形.