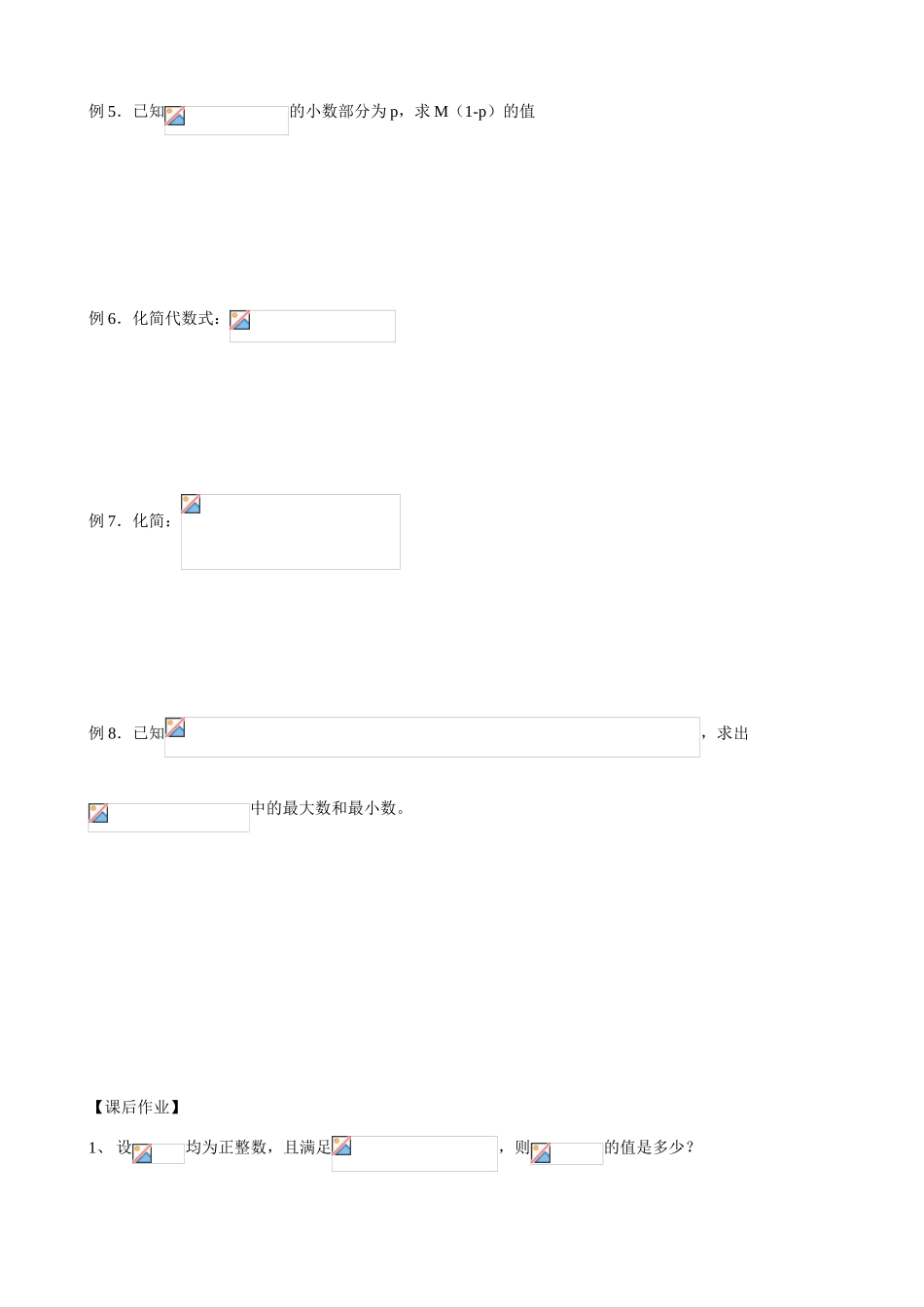
初三数学秋季提优第4讲二次根式感谢上帝没有把我造成一个灵巧的工匠,我的那些最主要的发现是受到失败的启发而获得的。——戴维【知识要点】1.了解二次根式的概念及其加、减、乘、除运算法则;2.会用运算法则进行有关实数的四则运算;3.通过观察、尝试、归纳、类比体验法则的产生过程,发展思维,培养创新、探究能力。【基础过关】1.下列数中,最小的正数是()A.B.C.D.2.下列说法正确的是()A.两个无理数之和是无理数B.两个无理数之积是无理数C.一个无理数与一个有理数之和是无理数D.无理数是开方开不尽的数3.已知,,,则的大小关系是()A.B.C.D.4.已知满足,则的取值范围是()A.B.C.D.以上都不对5.已知,则多项式的值是()A.0B.-1C.1D.6.设为有理数,且等式成立,则的值是()A.2005B.2006C.2007D.不能确定7.若满足,则________________.8.设均为不小于3的实数,则的最小值是________.9.已知是的立方根,是的相反数,且,那么的平方根是10.若和都是有理数,则()A.都是有理数B.都是无理数C.都是有理数或都是无理数D.中有理数和无理数各一个11.计算所得的结果是.12.若实数使等式成立,则。【典型例题】例1.若,则等于多少?例2.求的值例3.设,,则等于多少?例4.设正整数满足,则这样的的取值情况()A.有一组B.有两组C.多于两组D.不存在例5.已知的小数部分为p,求M(1-p)的值例6.化简代数式:例7.化简:例8.已知,求出中的最大数和最小数。【课后作业】1、设均为正整数,且满足,则的值是多少?2、化简:3、已知是实数,,则的值是多少?4、化简5、已知,且,则化简6、的值是多少?7、若,则化简8、当,代数式化简