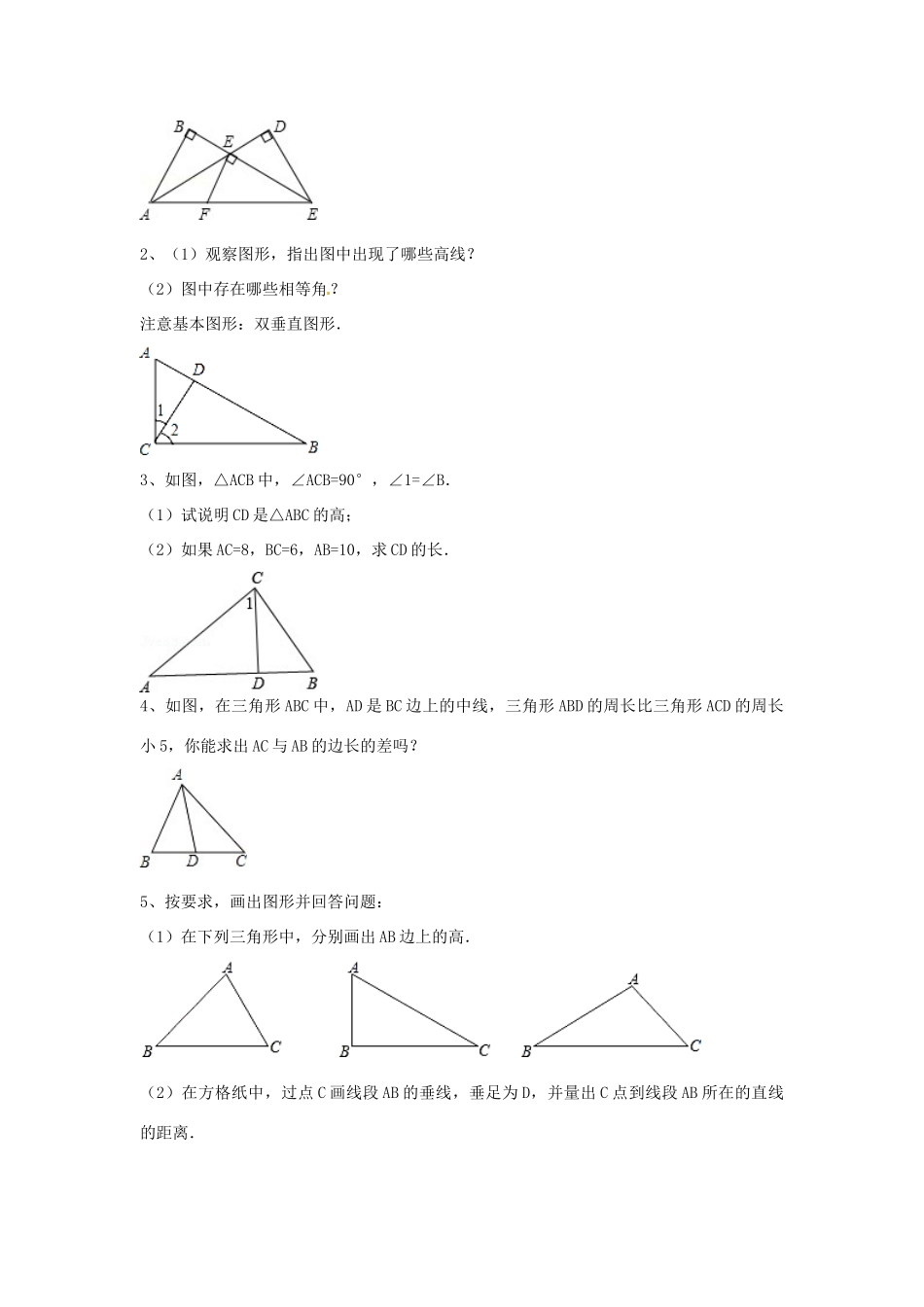
三角形一、教学目标:1.理解三角形的定义,了解三角形的稳定性和四边形的不稳定性。2.掌握三角形的边的性质,并能灵活应用,解决相关问题3.三角形的有关重要线段.4.理解三角形的不同分类.二、知识梳理1.三角形的分类:三角形按边分类可分为不等边三角形和等腰三角形(等边三角形是等腰三角形的特殊情况);按角分类可分为锐角三角形、直角三角形和钝角三角形,其中锐角三角形、钝角三角形统称为斜角形。2.三角形的边的性质(1)边与边的关系:三角形中任两边之和大于第三边,任两边之差小于第三边。三角形的三边:三角形的两边之和大于第三边;两边之差小于第三边;△ABC的三边a、b、c中已知a、b,求c的取值范围是:a-b<c<a+b;3.三角形的三线:三角形的所有高线、中线、角平分线:重心:三:典型练习和例题知识点:边的性质1.三角形两条边分别是2cm,7cm,则第三边c的范围2.等腰三角形的一边长为6cm,另一边长为12cm,则其周长3.用7根火柴首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数为4.等腰三角形一边的长是3,另一边的长是8,则它的周长是5.一个三角形的两边长分别是2cm和9cm,第三边的长为奇数,则第三边的长为_____.变式1:若边长是5cm和9cm呢?变式2:若周长为奇数呢?对应练习:配套第一课时例题1:用一条长为18㎝的细绳围成一个等腰三角形。(1)如果腰长是底边的2倍,那么各边的长是多少?(2)能围成有一边长为4㎝的等腰三角形吗?为什么?钝角三角形锐角三角形直角三角形三角形分析:(1)等腰三角形三边的长是多少?若设底边长为x㎝,则腰长是多少?(2)“边长为4㎝”是什么意思?解:(1)设底边长为x㎝,则腰长2x㎝。x+2x+2x=18解得x=3.6所以,三边长分别为3.6㎝,7.2㎝,7.2㎝.(2)如果长为4㎝的边为底边,设腰长为x㎝,则4+2x=18解得x=7如果长为4㎝的边为腰,设底边长为x㎝,则2×4+x=18解得x=10因为4+4<10,出现两边的和小于第三边的情况,所以不能围成腰长是4㎝的等腰三角形。由以上讨论可知,可以围成底边长是4㎝的等腰三角形。学生活动:学生先独立完成以上题目引导:请根据以上问题进行总结:对于三角形的边的性质,有哪几种题型进行考查,应注意什么问题?教师引导总结:题型1:知道三条线段,判断能否组成三角形。题型2:知道2边,求第三边的取值范围,或者周长的取值范围题型3:知等腰三角形的两边,求等腰三角形的周长,或者反之。注意两解问题。知识点:三线3.如图,已知:AD是△ABC的中线,△ABC的面积为80,,则△ABD的面积是.1、如图:(1)在△ABC中,BC边上的高是_________.(2)在△AEC中,AE边上的高是_________.(3)在△FEC中,EC边上的高是_________.(4)若AB=CD=2cm,AE=3cm,则S△AEC=_________cm2,CE=_________cm.ABDC2、(1)观察图形,指出图中出现了哪些高线?(2)图中存在哪些相等角?注意基本图形:双垂直图形.3、如图,△ACB中,∠ACB=90°,∠1=∠B.(1)试说明CD是△ABC的高;(2)如果AC=8,BC=6,AB=10,求CD的长.4、如图,在三角形ABC中,AD是BC边上的中线,三角形ABD的周长比三角形ACD的周长小5,你能求出AC与AB的边长的差吗?5、按要求,画出图形并回答问题:(1)在下列三角形中,分别画出AB边上的高.(2)在方格纸中,过点C画线段AB的垂线,垂足为D,并量出C点到线段AB所在的直线的距离.(3)过△ABC的顶点C,画MN∥AB,再过△ABC的边AB的中点D,画平行于AC的直线,交BC于点E.6、如图,在ABC中,AE是中线,AD是角平分线,AF是高,填空:(1)BE=_________=_________(2)∠BAD=__________________(3)∠AFB=_________=90°(4)S△ABC=_________S△ABE.7、如图,已知△ABC的高AD,角平分线AE,∠B=26°,∠ACD=56°,求∠AED的度数.8、如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差.9、如图所示,AD是△ABC的中线,AE是△ACD的中线,已知DE=2cm,求BD,BE,BC的长.10、如图,△ABC中,∠ABC=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.(1)求∠DAE的度数;(2)指出AD是哪几个三角形的高.11、在△ABC中,AD是BC边上的中线,若△ABD和△ADC的周长之差为4...