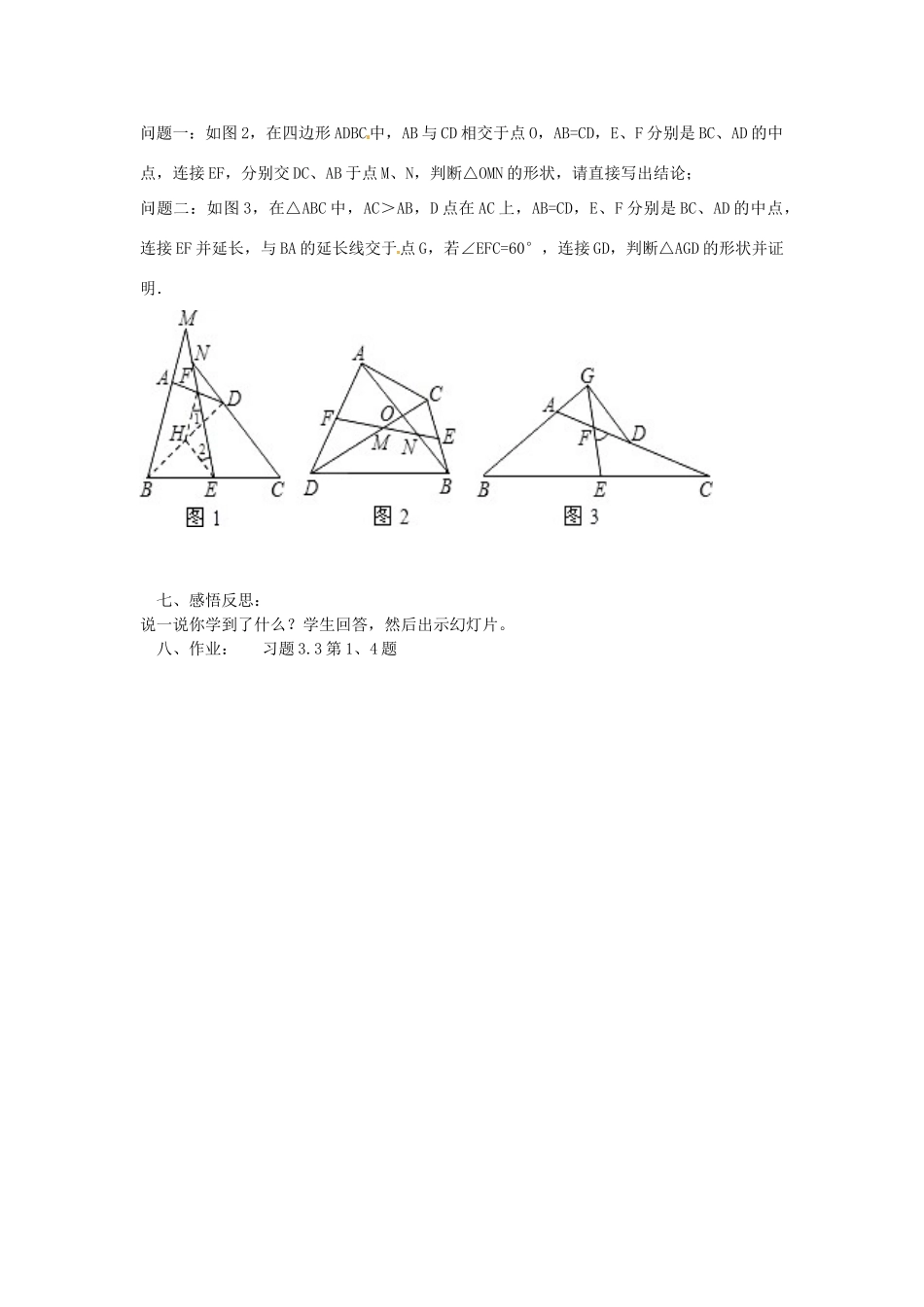
山西省太谷县明星中学八年级数学上册《三角形的中位线》教案(3)北师大版教学目标:1.知识与技能通过画图,亲身体验三角形中位线的概念以及与三角形中线的区别,掌握三角形中位线定理,通过三角形中位线定理的证明,渗透数学学习中的转化思想,培养学生自主探究、猜想、推理论证的能力,并能应用所学的知识解决问题。2.过程与方法通过问题让学生猜想三角形的中位线与第三边的关系,进而用推理论证的方法证明猜想是否正确。3、情感、态度与价值观:培养学生的推理论证的能力和水平,并进一步培养学生的协作精神和创新思维能力。教学重点、难点1.重点:三角形的中位线定理以及定理的证明过程,应用三角形中位线定理解决问题。2.难点:证明三角形中位线定理如何添加辅助线是本节的教学难点。教学过程一.自主探究:1.你能将任意一个三角形分成四个全等的三角形吗?请同学们拿出自己准备好的三角形纸片试着分一下(先独立完成,然后交流)学生回答:你是怎样做的?(连接每两边的中点)提问:你认为这样做对吗?教师演示学生做的,把四个三角形折叠在一起,四个三角形完全重合。本节课我们来研究一下三角形中位线定理。(板书课题)二、设问导读:(1)三角形有几条中线?它们是什么点间的连线?在图中,若D、E、F分别是AB、AC、BC中点,请同学们在图中,连结DE、DF、EF,(2)提问:这三条线段都是什么点间的连线?这三条线段称为△ABC的中位线.你能否根据刚才的画图,写出三角形中位线的定义呢?(3)说说三角形的中线和三角形的中位线的异同?(都是线段,都有三条,一个是顶点与对边中点的连线,一个是两边中点的连线)(4)如图,DE是△ABC的中位线,那么请同学们观察一下,猜一猜:中位线DE与BC在位置和数量上各有什么关系?为了猜想中位线DE与BC在位置和数量上各有什么关系,我们做一个拼图活动:出示(活动一):我们把三角形沿中位线DE剪一刀.试一试:你能不能把△ADE和四边形BDEC拼接成一个平行四边形呢?你也可以与同桌合作,共同探索,一起来拼.我们把刚才拼接好的平行四边形画在练习纸上,请同学们打开,然后小组讨论一下,请把你论写在纸上.三、点拨展示:1.刚才同学们交流了利用我们所提供的图形,得到了中位线DE与BC在位置和数量上的关系,你能否用语言叙述这一结论呢?命题:三角形的中位线平行于第三边,并且等于第三边的一半.2、你能证明这个命题吗?(板书)已知:如图,在△ABC中,AD=DB,AE=EC.求证:DE∥BC,DE=1/2BC(经过交流、分析后,学生独立写出证明过程)通过了同学们的证明,可以知道你们猜想的结论是正确的.我们把这个结论称为三角形中位线定理,(把命题改写成三角形中位线定理)三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半.已知:如图所示,在△ABC中,AD=DB,AE=EC求证:DE∥BC,证明:延长DE到F,使EF=DE,连结CF, AE=CE,∠AED=∠CEF(对顶角相等),ED=EF∴△ADE≌△CFE(SAS)AD=CF(全等三角形的对应边相等)∠ADE=∠F(全等三角形的对应角相等)∴AD∥CF(内错角相等,两直线平行) AD=DB,∴CF=DB所以四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)于是DF∥BC,DF=BC,即DE∥BC,DE=1/2BC。四、自我检测①已知三角形三边长分别为6,8,10,顺次连接各边中点所得的三角形周长是多少?②如果三边的长分别为a、b、c,那么顺次连接各边中点所得的三角形周长是多少?③已知三角形的面积是S,顺次连接各边中点所得的三角形面积是多少?五、题组练习:1、已知:如果,点D、E、F分别是△ABC的AB、AC、BC边的中点.(1)若AB=8cm,求EF的长;(2)若DE=5cm,求BC的长.(3)若增加M、N分别是BD、BF的中点,问MN与AC有什么关系?为什么?三角形中位线定理不仅有三角形的中位线与第三边之间的位置关系,而且还有它们之间的数量关系.另外,从第(3)题可知:当题设中出现中点时,要考虑应用三角形中位线定理来解决.2、如图:A、B两地被池塘隔开,现要测量出A,B两地的距离,给你的工具只有皮尺,你能想办法测量出来吗?六、拓展延伸:如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF...