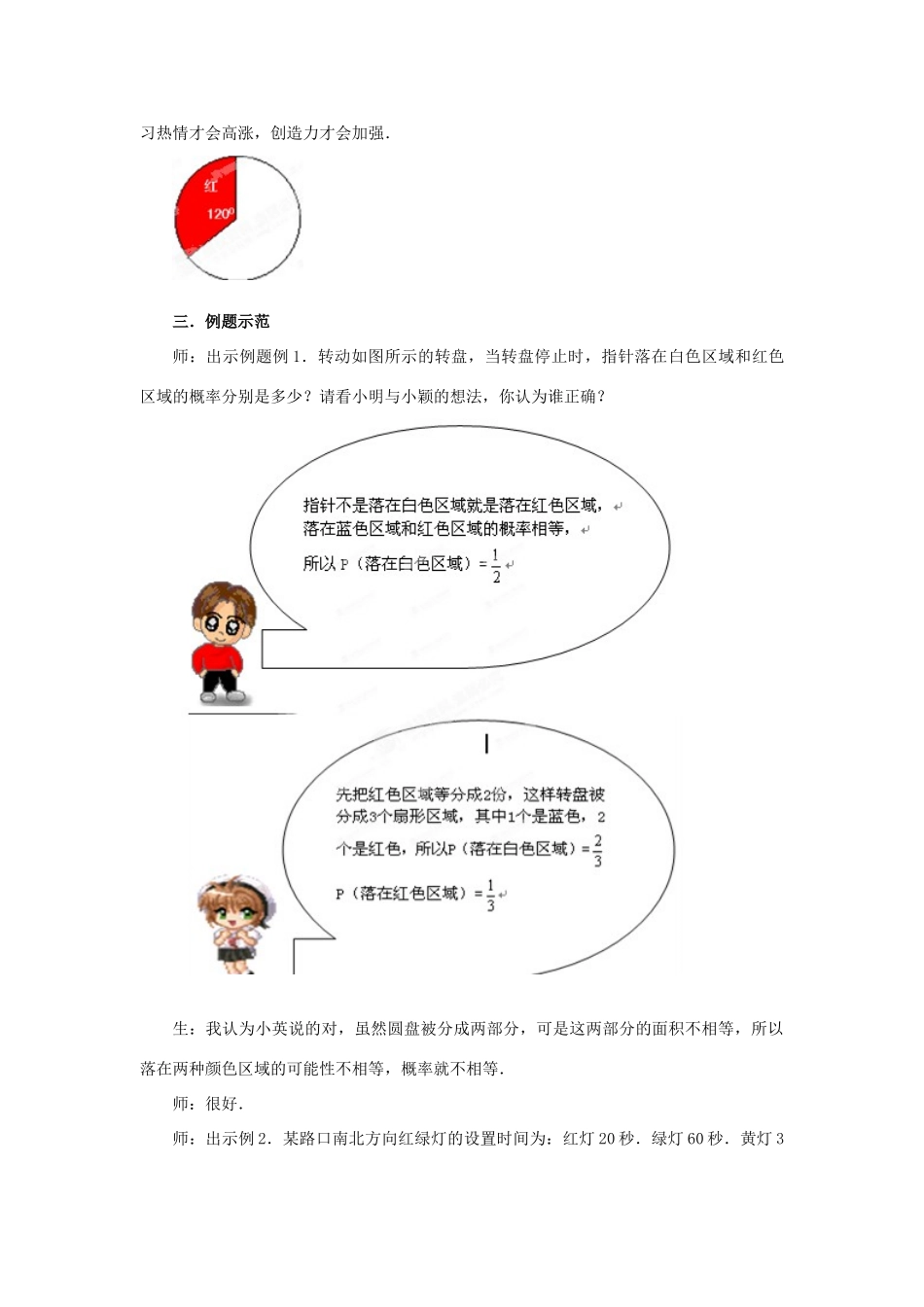
6.3.4等可能事件的概率教案教学目标1.了解概率的意义,了解常用的概率研究模式之一:“几何概率模型”,会进行简单的概率计算,了解概率的大小与面积的关系,能设计符合要求的简单概率模型.2.在分组讨论合作探究的过程中体会事件发生的不确定性,进一步体会“数学就在我们身边”.3.初步认识概率与人类生活的密切联系,感受概率的应用价值,增强学生学数学.用数学的意识,提高学生之间的合作交流能力和学习数学的兴趣.教学重点与难点:重点:会进行简单的概率计算,了解概率的大小与面积的关系,能设计符合要求的简单概率模型.难点:构造“几何概率模型”,会进行简单的概率计算.教法与学法指导:教师指导学生进行“猜想→实验→分析→交流→发现→应用”的一系列活动,积极思考,独立探索,自己发现并掌握相应的规律.通过具体的现实情境,从学生已有的生活经验出发,通过“猜想→实验→分析→交流→发现→应用”,经历自主探索.分组实验.合作交流等活动形式,以学生为主体,教师创设和谐,愉悦的环境,辅以适当的引导.同时利用计算机演示教学内容,提高教学的交互性与直观性,打破教学常规,提高课堂效率.教学过程一.回顾与思考师:回顾前面学过的有关知识.1.什么是概率?2.如何计算一个事件的概率?生1:如果一个事件有n种可能结果,事件A包含其中m种结果,那么事件A发生的概率为.生2:重点求公式中的m,n的值.设计意图:“学生原有的知识和经验是教学活动的起点”,通过复习古典概型.几何概型的计算方法,使学生在学习本节知识前扫清障碍,并起到承上启下的作用.二.问题的引出师:出示讨论题目:如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和红色区域的概率分别是多少?生:独立思考.书写答案,然后小组交流,最后全班展示,教师总结.生:以下三种答案:方案一:指针不是落在蓝色区域就是落在红色区域,落在蓝色色区域和红色区域的概率相等,所以P(落在蓝色区域)=P(落在红色区域)=.方案二:先把红色区域等分成2份,这样转盘被分成3个扇形区域,其中1个是蓝色,2个是红色,所以P(落在蓝色区域)=,P(落在红色区域)=.方案三:利用圆心角度数计算,所以P(落在蓝色区域)=,P(落在红色区域)==结论:转盘应被等分成若干份.各种结果出现的可能性务必相同.设计意图:苏霍姆林斯基说过:“应该让我们的学生在每一节课上都感到热烈的.沸腾的.多姿多彩的精神生活.”课堂上,只有让学生真正“动”.“活”起来,学生的学习热情才会高涨,创造力才会加强.三.例题示范师:出示例题例1.转动如图所示的转盘,当转盘停止时,指针落在白色区域和红色区域的概率分别是多少?请看小明与小颖的想法,你认为谁正确?生:我认为小英说的对,虽然圆盘被分成两部分,可是这两部分的面积不相等,所以落在两种颜色区域的可能性不相等,概率就不相等.师:很好.师:出示例2.某路口南北方向红绿灯的设置时间为:红灯20秒.绿灯60秒.黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:(1)他遇到红灯的概率大还是遇到绿灯的概率大?(2)他遇到红灯的概率是多少?生:(1)遇到红灯的概率大.生:(2)设计意图:通过上一环节学生已经了解了几何概型公式计算的前提是各种结果出现的可能性务必相同.此时出示这两道例题,是让学生达到学以致用的目的.注意在此环节仍需给学生充分的时间解决问题.四.巩固练习师:看谁答对的问题多,若问题回答正确,则可打开一扇门.1.一位汽车司机准备去商场购物,然后他随意把汽车停在某个停车场内,停车场内一个停车位置正好占一个格且每个格除颜色外完全一样,则汽车停在蓝色区域的概率.2.一张写有密码的纸片被随意地埋在下面矩形区域内(每个方格大小相同)(1)埋在哪个区域的可能性大?(2)分别计算出埋在三个区域内的概率;(3)埋在哪两个区域的概率相同.3.如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率.(指针恰好指向两扇形交线的概率视为零).[来源:学科网ZXX...