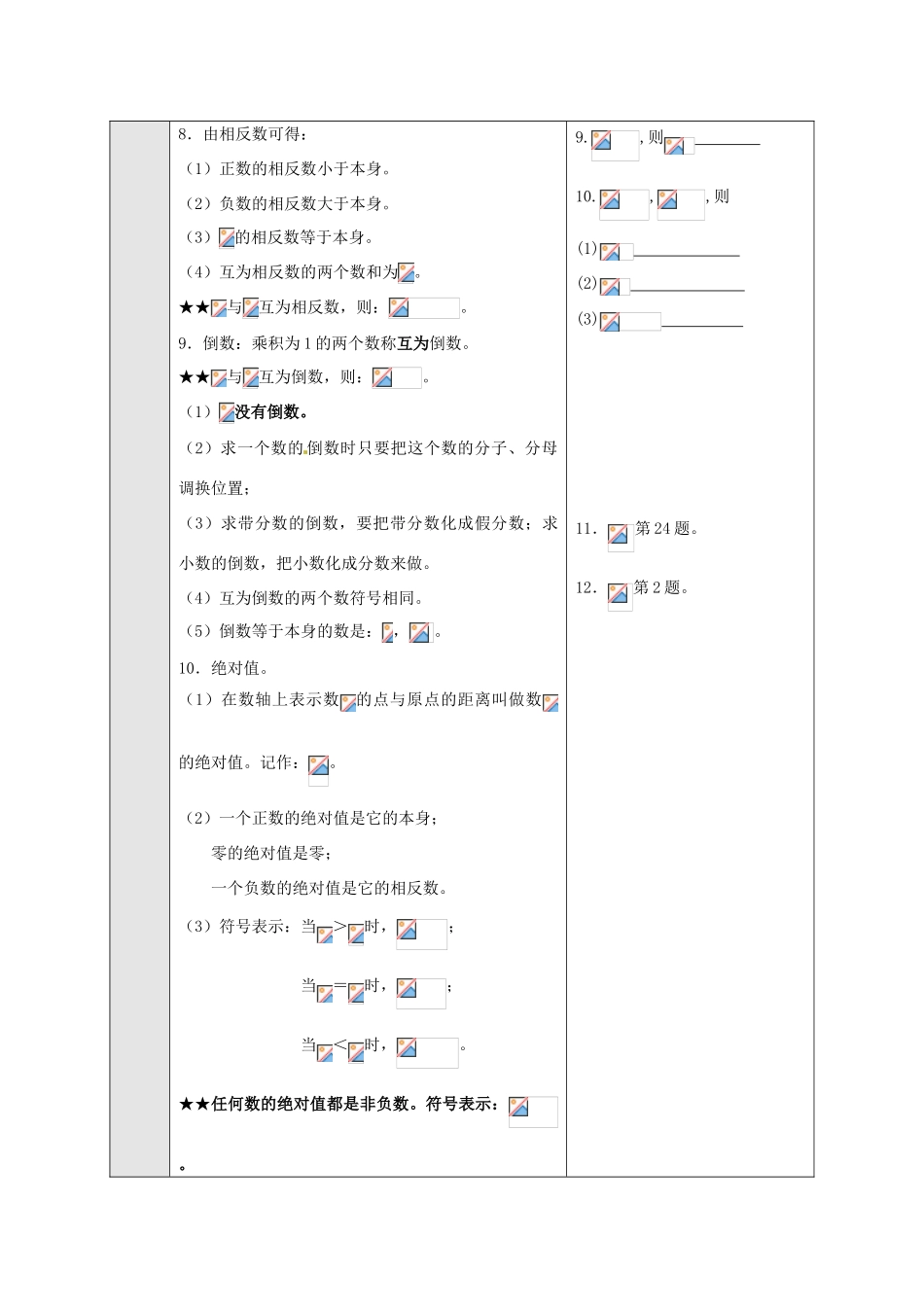
四川省宜宾市南溪二中七年级数学上册《第一章有理数》复习教案人教版教学目标1、理解有理数的意义,并能用数轴上的点表示有理数,会比较有理数的大小。2、借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值。3、会求有理数的倒数。教学重点理解有理数的概念。教学难点有理数大小的比较及绝对值的概念。教学过程学生活动新课解析及例题精讲一、知识点巩固:1.正数和负数。注意:0既不是正数也不是负数。2.有理数的两种分类。(1)“非…集”的理解。(2)小数与分数的转化。有限小数和无限循环小数可以转化成分数,因此它们是有理数。(3)无限不循环小数不能转化成分数,因此不是有理数,如:,我们称它为无理数。3.数轴。(1)数轴的三要素:原点,正方向,单位长度。(2)数轴是一条直线,而不是射线。(3)在数轴上表示有理数时,数写在对应刻度的正上方。对应刻度用小黑点涂黑。注意:分数和带分数的表示方法。4.有理数的大小比较。方法一:在数轴上表示的两个数,右边的数总比左边的数大。方法二:正数都大于;负数都小于;1.(1)判断:带有“-”的数就是负数。(2)第1题。(3)第22题。2.将下列各数分别填入相应的大括号内。,,,,,,,,,,正有理数集:{…}整数集:{…}非负整数集:{…}正分数集:{正数大于一切负数;两个负数,绝对值大的反而小。注意:(1)在比较有理数的大小时,注意观察是否有需要化解的数。如:,等。(2)在用方法二比较两个有理数的大小时,注意先观察两个有理数的符号。5.从数轴上观察得出:(1)有最小的正整数:;没有最大的正整数。(2)有最大的负整数:;没有最小的负整数。(3)没有最小的整数;也没有最大的整数。(4)有最小的自然数:;没有最大的自然数。(5)没有最小的正数;也没有最大的负数。6.(1)求数轴上两点之间的距离:较大的数-较小的数。(2)求数轴上的点向左(右)移动后所表示的数:向右“”,向左“-”。7.相反数。(1)代数意义:只有正负号不同的两个数称互为相反数。也称其中一个数是另一个数的相反数。(2)几何意义:在数轴上表示互为相反数的两个点分别位于原点的两边,且与原点的距离相等。(3)零的相反数是零。(4)在一个数的前面添“-”,表示这个数的相反数;在一个数的前面添“”,表示这个数的本身。(5)多重符号的化解:数“-”的个数。(6)一个数的相反数的相反数等于这个数的本身。…}3.第3(比较方法一)、4(比较方法二)、5、6题。注意:用“<”或“>”连接一组数据时,只能出现其中一种符号,不能既有“<”又有“>”。4.第18题。(求距离)5.-(-4)的相反数是_______,-(+8)是______的相反数.6.第10题。(相反数)7.第17题。(倒数)8.若的倒数与互为相反数,则等于。8.由相反数可得:(1)正数的相反数小于本身。(2)负数的相反数大于本身。(3)的相反数等于本身。(4)互为相反数的两个数和为。★★与互为相反数,则:。9.倒数:乘积为1的两个数称互为倒数。★★与互为倒数,则:。(1)没有倒数。(2)求一个数的倒数时只要把这个数的分子、分母调换位置;(3)求带分数的倒数,要把带分数化成假分数;求小数的倒数,把小数化成分数来做。(4)互为倒数的两个数符号相同。(5)倒数等于本身的数是:,。10.绝对值。(1)在数轴上表示数的点与原点的距离叫做数的绝对值。记作:。(2)一个正数的绝对值是它的本身;零的绝对值是零;一个负数的绝对值是它的相反数。(3)符号表示:当>时,;当=时,;当<时,。★★任何数的绝对值都是非负数。符号表示:。9.,则10.,,则(1)(2)(3)11.第24题。12.第2题。绝对值最小的有理数是:。11.由绝对值可得:(1)互为相反数的两个数的绝对值相同。(2)绝对值相等的两个数相等或互为相反数。(3)几个非负数(绝对值,偶次幂)的和为,则每个非负数都为。二、例题解析:【例1】在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东处,商场在学校西处,医院在学校东处。若将马路近似地看作一条直线,以学校为原点,向东方向为正方向,用个单位...