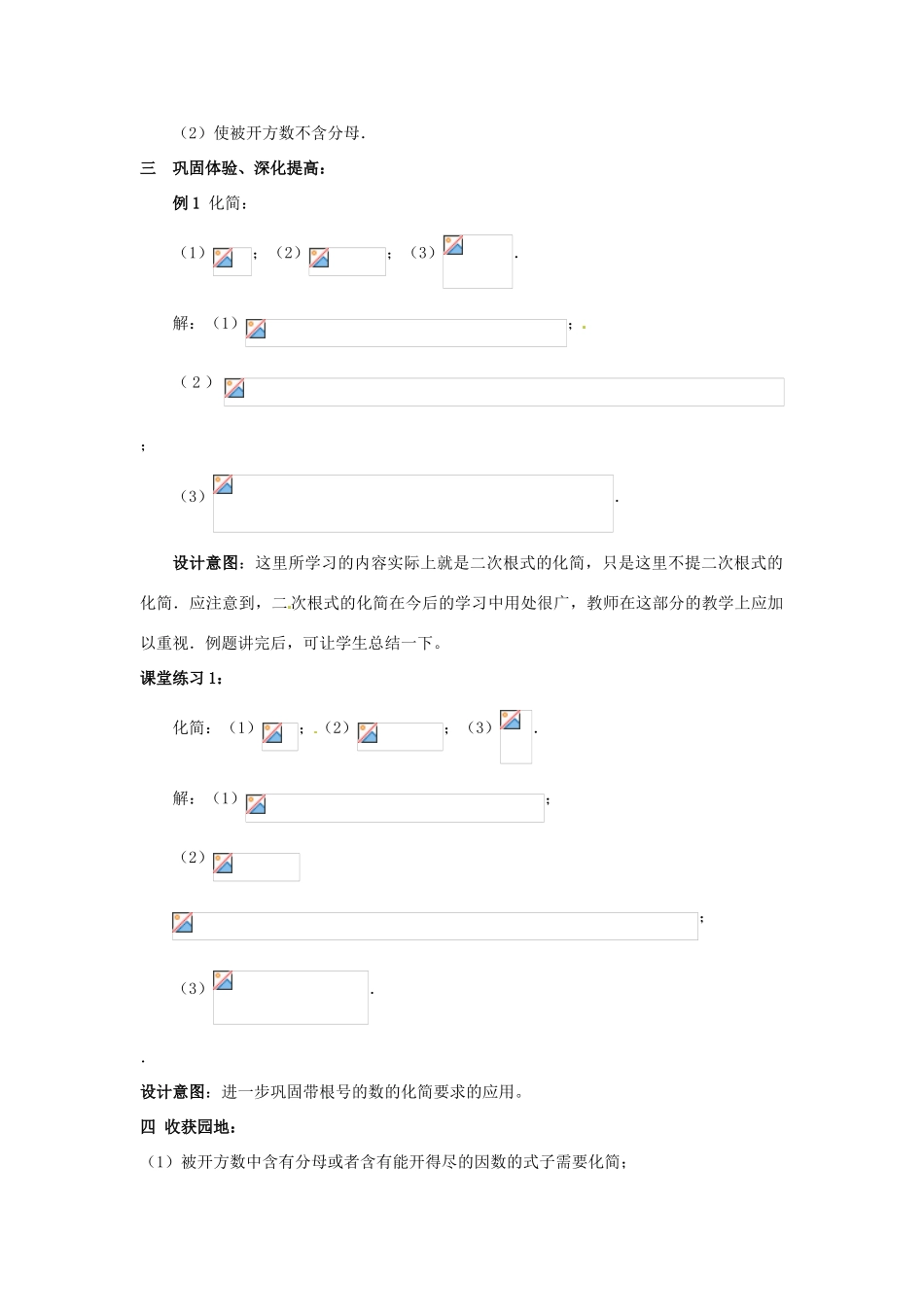
山东省枣庄市峄城区吴林街道中学八年级数学上册《2.6实数》教案2北师大版(2)课前准备:制作课件,学生课前进行相关调查及预习工作.教学过程:一创设问题情境、引入新课:师:1.算术平方根的概念?生:回答2.下面正方形的边长分别是多少?师:这两个数之间有什么关系,你能借助什么运算法则或运算率解释它吗?【点明本节课研究课题】设计意图:借助复习,在巩固旧知的同时,导入新课。二分组展示、探究总结:1.明晰上一课时探究的公式:(a≥0,b≥0),(a≥0,b面积8面积2>0).师:能否根据该公式将化成?生探究转化方法,并明晰这实际上是将公式反用,建立知识之间的联系。2.巩固练习:化简:(1);(2);(3);(4);(5).答案:(1);(2);(3);(4);(5).师:含有根号的数与一个不含根号的数相乘,一般把不含根号的数写在前面,并省略去乘号.师:事实上,对带有根号的数的化简,不仅仅限于以上提出的要求,它还有其他要求.如就需要化简.怎样化简呢?同学们可互相讨论一下.生探究:化简:.原来被开方数含有分母,化简后,被开方数不含分母了.3.练习:化简:.生归纳:带根号的数的化简要求:(1)使被开方数不含开得尽的数;(2)使被开方数不含分母.三巩固体验、深化提高:例1化简:(1);(2);(3).解:(1);(2);(3).设计意图:这里所学习的内容实际上就是二次根式的化简,只是这里不提二次根式的化简.应注意到,二次根式的化简在今后的学习中用处很广,教师在这部分的教学上应加以重视.例题讲完后,可让学生总结一下。课堂练习1:化简:(1);(2);(3).解:(1);(2);(3)..设计意图:进一步巩固带根号的数的化简要求的应用。四收获园地:(1)被开方数中含有分母或者含有能开得尽的因数的式子需要化简;(2)公式(a≥0,b≥0),(a≥0,b>0)从左往右或从右往左在化简中会灵活运用.五课后作业:习题2.10T(1)六板书设计第六节实数(3)一、导入二、新课三、例题讲解四、补充练习五、课时小节六、课后作业七、教学反思对于实数的运算,本教材没有提出过高的要求.对于大多数学生,只要能完成教材上介绍的类型的计算即可,不要出现过于繁琐和复杂题目和类型.当然,如果学生通过这个课时还没有掌握课本上对化简的要求,也不妨增加1个课时,进行巩固训练。本节课的教学设计中考虑了学生的层次不同,对知识的要求也不同,因此增加了知识拓展的内容,供层次高一些的学