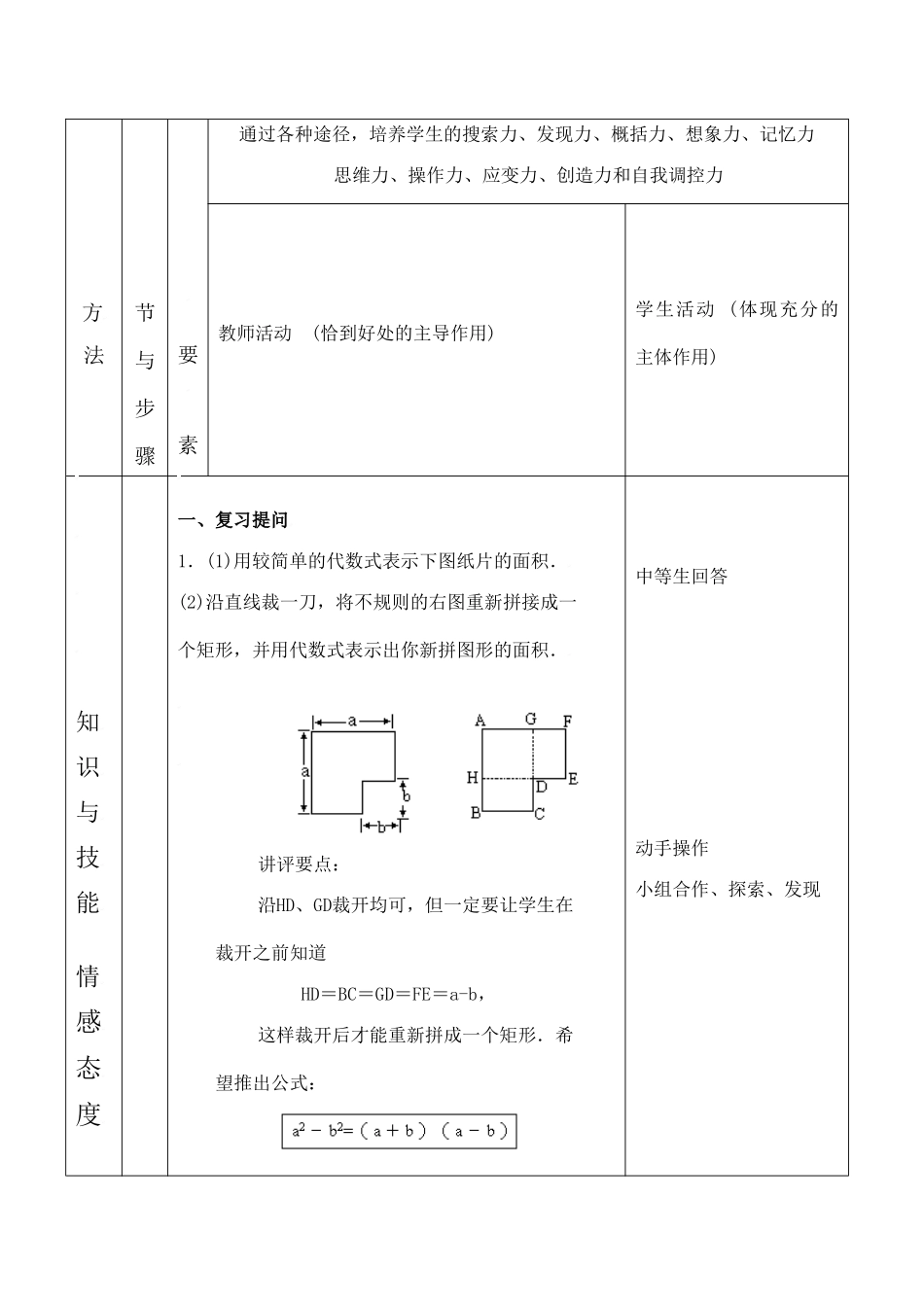
昆明南洋中学部执行新课标新授课教案模板(2009至2010学年下学期)教案序号总第12课时(一课一个教案)教学课题平方差公式(二)三维目标知识目标进一步使学生理解掌握平方差公式,并通过小结使学生理解公式数学表达式与文字表达式在应用上的差异.能力目标进一步培养学生分析、归纳和探索能力情感目标培养学生数形结合的思想教学重、难、疑点公式的应用及推广教学方法教法引导探索研究发现法学法主动探索研究发现法教具学具准备剪刀、正方形纸片教学过程设计巧设情景导入新课见过程过程与教学环课堂充分体现“自主、合作,分层评价”(渗透探究的内涵)的教学特色(力求课堂活而不乱,实而不闷)“知识是能力的基础,能力是知识的升华,情感是力量的源泉”方法节与步骤要素通过各种途径,培养学生的搜索力、发现力、概括力、想象力、记忆力思维力、操作力、应变力、创造力和自我调控力教师活动(恰到好处的主导作用)学生活动(体现充分的主体作用)知识与技能情感态度一、复习提问1.(1)用较简单的代数式表示下图纸片的面积.(2)沿直线裁一刀,将不规则的右图重新拼接成一个矩形,并用代数式表示出你新拼图形的面积.讲评要点:沿HD、GD裁开均可,但一定要让学生在裁开之前知道HD=BC=GD=FE=a-b,这样裁开后才能重新拼成一个矩形.希望推出公式:中等生回答动手操作小组合作、探索、发现与价值观2.(1)叙述平方差公式的数学表达式及文字表达式;(2)试比较公式的两种表达式在应用上的差异.说明:平方差公式的数学表达式在使用上有三个优点.(1)公式具体,易于理解;(2)公式的特征也表现得突出,易于初学的人“套用”;(3)形式简洁.但数学表达式中的a与b有概括性及抽象性,这样也就造成对具体问题存在一个判定a、b的问题,否则容易对公式产生各种主观上的误解.依照公式的文字表达式可写出下面两个正确的式子:经对比,可以让人们体会到公式的文字表达式抽象、准确、概括.因而也就“欠”明确(如结果不知是谁与谁的平方差).故在使用平方差公式时,要全面理解公式的实质,灵活运用公式的两种表达式,比如用文字公式判断一个题目能否使用平方差公式,用数学公式确定公式中的a与b,这样才能使自己的计算即准确又灵活.3.判断正误:(1)(4x+3b)(4x-3b)=4x2-3b2;(×)通过对比、观察、全面理解公式的实质,灵活运用公式的两种表达式(2)(4x+3b)(4x-3b)=16x2-9;(×)二、新课例1运用平方差公式计算:(1)102×98;(2)(y+2)(y-2)(y2+4).例2填空:(1)a2-4=(a+2)();(2)25-x2=(5-x)();(3)m2-n2=()();思考题:什么样的二项式才能逆用平方差公式写成两数和与这两数的差的积?(某两数平方差的二项式可逆用平方差公式写成两数和与这两数的差的积)例3计算:(1)(a+b-3)(a+b+3);(2)(m2+n-7)(m2-n-7).三、小结1.什么是平方差公式?一般两个二项式相乘的积应是几项式?2.平方差公式中字母a、b可以是那些形式?3.怎样判断一个多项式的乘法问题是否可以用平方差公式?尝试、交流、教师点拨小组讨论尝试、交流、教师点拨学生自己总结精选课堂练习基础题有广度(投影显示或书面练习)提高题有梯度(投影显示或书面练习)(习题适应全体学生)见过程(习题适应不同层次的学生)巧布课外作业1.运用平方差公式计算:(1)(a2+b)(a2-b);(2)(-4m2+5n)(4m2+5n);(3)(x2-y2)(x2+y2);(4)(9a2+7b2)(7b2-9a2).2.运用平方差公式计算:(1)69×71;(2)53×47;