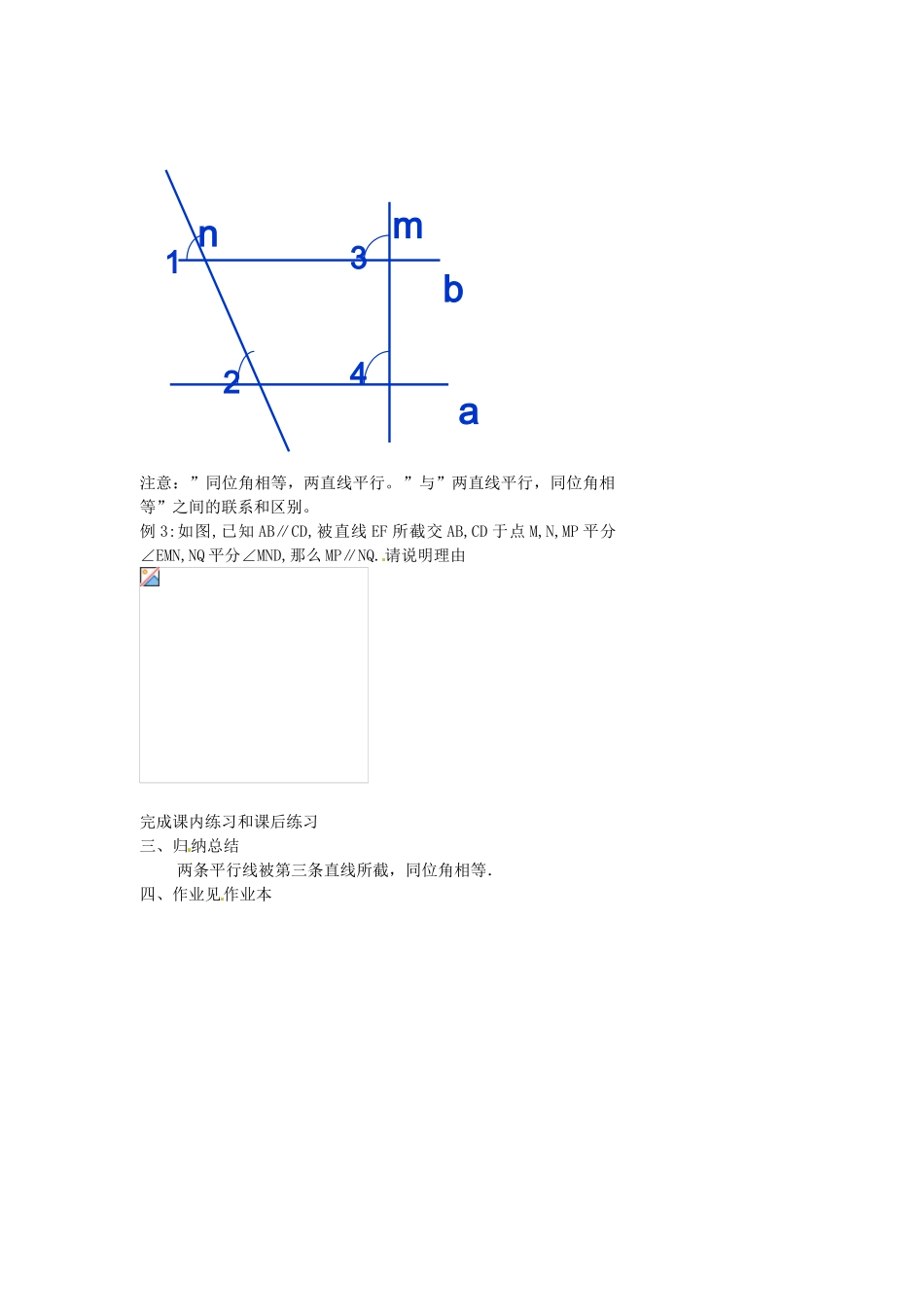
1.3平行线的性质(1)【教学目标】一、知识和技能1.理解平行线的性质与平行线的判定是相反问题.2.掌握平行线的性质.3.应用会用平行线的性质进行推理和计算.二、过程与方法1.通过画平行线、度量角培养学生实际操作能力(即画图测量的能力).2.通过平行线性质定理的推导,培养学生的观察分析和进行简单的逻辑推理能力.三、情感、态度与价值观通过学习平行线的性质与判定的联系与区别,培养学生事物是普遍联系又是相互区别的辩证唯物主义思想.【教学重点与难点】教学重点:平行线的性质公理及平行线性质定理的推理.教学难点:平行线性质与判定的区别及推理过程.【教学方法】采用尝试指导,引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.【教学过程】一、探索新知、讲授新课师:我们都知道平行线的画法,请同学们画出直线AB的平行线CD,结合画图过程思考画出的平行线,已有一对同位角的关系是怎样的?学生活动:学生在练习本上画图并思考.学生画图的同时教师在黑板上画出图形(见图2-61),当同学们思考时,教师有意识地重复演示过程.【教法说明】让同学们动手、动脑、观察思考,使学生养成自己发现问题得出规律的习惯.学生活动:学生能够在完成作图后迅速地答出已有一对同位角相等.提出问题:是不是每一对同位角都相等呢?请同学们任画一条直线E′F′,使它截平行线AB与CD,得同位角∠3、∠4,利用量角器量一下,∠3与∠4有什么关系?相关以往知识:________________________________________________________________________________________教学内容和方法:____________________________________________________________________________________________________________________________________个性化教学思路及改进建议:__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________学生活动:学生按老师的要求画出图形,并进行度量,回答出不论怎样画截线,所得的同位角都相等.根据学生的回答,教师肯定结论.师:两条直线被第三条直线所截,如果这两条直线平行,那么同位角相等.我们把平行线的这个性质作为公理.[板书]两条平行线被第三条直线所截,同位角相等.简单说成,两直线平行,同位角相等.二、尝试反馈,巩固练习例1如图:梯子的各条横档互相平行,∠1=100o,求∠2的度数。注重两种分析法:即从条件分析法和从结论出发的方法例2如图:已知∠1=∠2。若直线b⊥m,则直线a⊥m。请说明理由。__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________注意:”同位角相等,两直线平行。”与”两直线平行,同位角相等”之间的联系和区别。例3:如图,已知AB∥CD,被直线EF所截交AB,CD于点M,N,MP平分∠EMN,NQ平分∠MND,那么MP∥NQ.请说明理由完成课内练习和课后练习三、归纳总结两条平行线被第三条直线所截,同位角相等.四、作业见作业本abmn1234